欧几里得算法
「欧几里得算法」(又称辗转相除法)用于计算两个数的最大公约数。
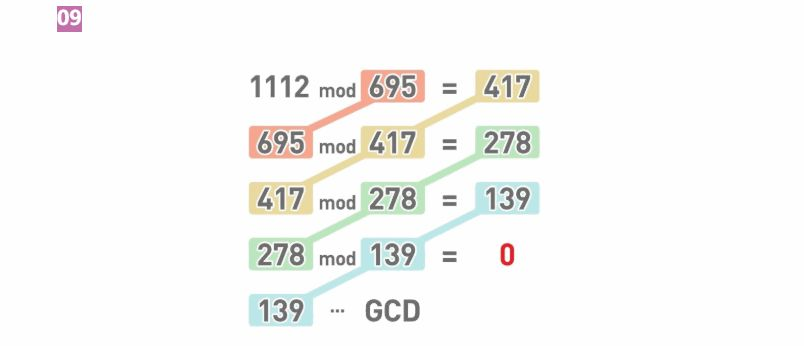
程首先用较大的数字去除以较小的数字,求出余数。也就是对两个数字进行mod运算。
A mod B就是算出A除以B后的余数C。例:1112 mod 695 =417,设A = 1112,B = 695。接下来再用被除数695和余数417进行mod运算。结果为278。
接下来再用除数695和余数417进行mod运算。结果为278。继续重复同样的操作,对417和278进行mod运算,结果为139。对278和139进行mod运算,结果为0。也就是说,278可以被139整除。
余数为0时,最后一次运算中的被除数139就是1112和695的最大公约数。
素性测试
素性测试判断一个自然数是否为素数的测试。素数(prime number)就是只能被1和其自身整除,且大于1的自然数。
费马测试被称为概率性素性测试,它判断的是“某个数是素数的概率大不大”。
「素数的性质(案例用素数5)」
对于比5小的数,分别计算它们的5次方

再对结果分别进行mod运算,求得它们除以5后的余数

观察原本的数和余数,发现两者一致。由此,可以推导出关于素数5,以上公式成立。

费马测试数字113是素数

补充知识如果p是素数,那么所有比p小的数n都满足np mod p=n这个条件。但反过来,即使所有n都满足条件,p也有可能不是素数。因为在极低概率下会出现所有n都满足条件的合数(非素数的自然数)。
比如数字561可以表示为3×11×17,所以561是合数,不是素数。然而比561小的所有数字都满足上述条件。这样的合数就叫作“卡迈克尔数”(Carmichael numbers),也叫“绝对伪素数”。
网页排名
网页排名(PageRank,也叫作佩奇排名)是一种在搜索网页时对搜索结果进行排序的算法。网页排名就是利用网页之间的链接结构计算出网页价值的算法。
汉诺塔
汉诺塔是一种移动圆盘的游戏,同时也是一个简单易懂的递归算法应用示例。
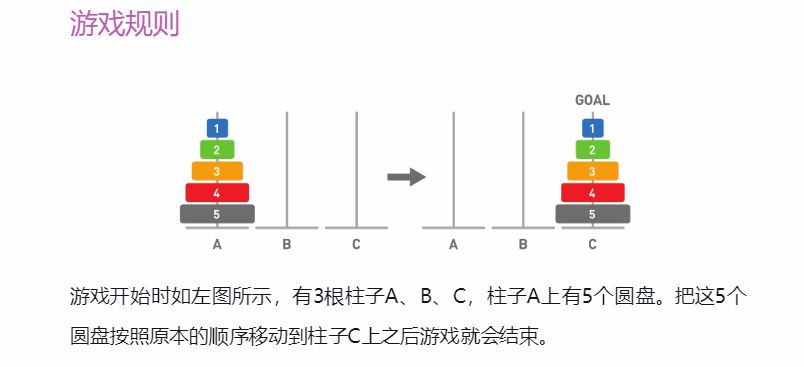
原理在算法描述中调用算法自身的方法就叫作“递归”。递归被运用到各种各样的算法中,这些算法统称为“递归算法”。
补充说明假设解决有n个圆盘的汉诺塔问题时需要的时间为T(n)。只有1个圆盘时只需1步就能完成,所以T(1)=1。圆盘数为n时,把上面的n-1个圆盘从A移到B上需要T(n-1),再把最大的圆盘移到C上需要1步,最后把B上的n-1个圆盘移到C上需要T(n-1),因此T(n)=2T(n-1)+1。
上面的公式即为T(n)=2n-1,这便是解决这个问题所需要的最短时间。
