🍕 单变量线性回归 Linear Regression with One Variable

一、模型表示

在监督学习里，我们有一个数据集，被称为训练集，

✍ 我们需要使用一些符号：

• m：表示训练样本的数量 Number of training examples

• x：输入变量 / 特征 input variable / features

• y：输出变量 / 目标变量 output variable / target variable

• (x，y)：一个训练样本 one training example

• ($x^{(i)}$，$y^{(i)}$)：第 i 个训练样本

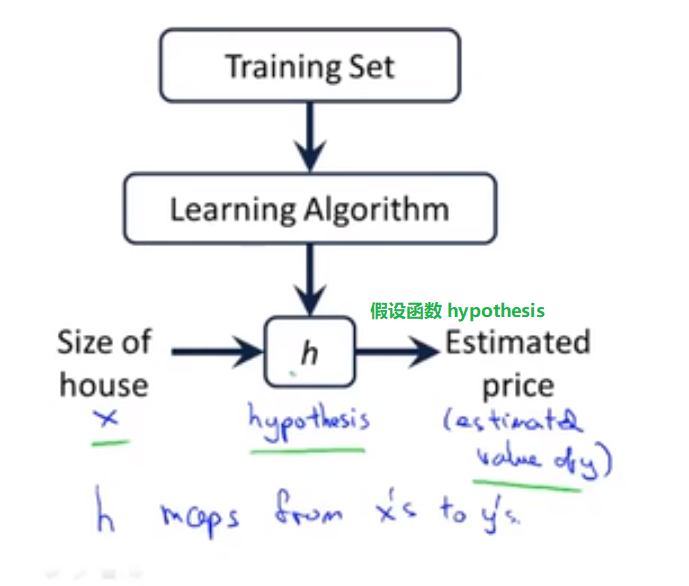
• h 代表学习算法的解决方案或函数也称为假设（hypothesis）

OK，如何给训练集下定义呢？我们先来了解监督学习算法是怎样工作的：

我们怎么表示我们的假设函数 hypothesis呢？这里我们选择最简单的假设函数作为我们接下来的函数：

🔢 $h_θ(x) = θ_0 + θ_1*x$

如果我们已有数据集输入数据 x 和输出数据 y，那么 🔴 假设函数的作用就是预测 y 是关于 x 的线性函数

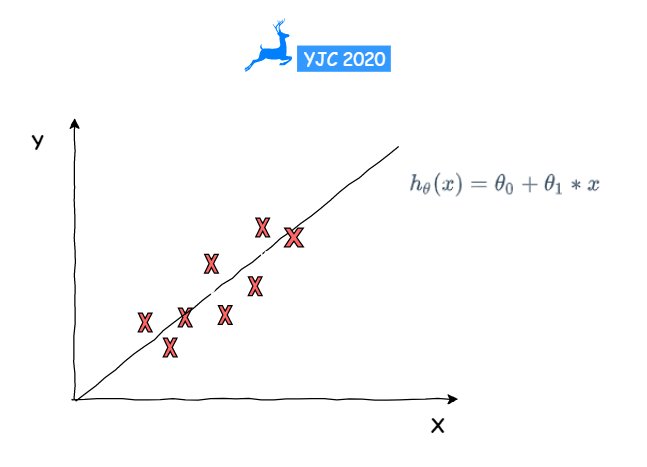
🔴 这种模型也被称为线性回归 linear regression，即拟合出一条直线最佳匹配我们所拥有的数据。上面这个例子是一元线性回归，即单变量 x 的函数，也称单变量 one variable 线性回归

二、代价函数 Cost function

对于假设函数：$h_θ(x) = θ_0 + θ_1*x$

θi 我们称之为模型参数，我们接下来要讲解的就是如何选择两个参数值 $θ_0$ 和 $θ_1$

我们会得到不同的假设，不同的假设函数

我们所要做的，就是求出参数值 $θ_0$ 和 $θ_1$ ，来让假设函数表示的直线最大程度的拟合我们的数据

🔴 我们给出标准的定义：在线性回归中，我们要解决的就是一个最小化问题 minimization，希望找到参数值 $θ_0$ 和 $θ_1$ 使得 $h_θ(x) - y$ 尽可能的小（即假设函数的值 / 预计输出值 与 实际输出值 尽可能的接近），那么我们需要做的事情就是尽量减少假设的输出 $h_θ(x)$ 与实际输出 y 之间的差的平方。

⭐⭐⭐ 通俗来说，通过使得代价函数的取得全局最小值，找出参数 $θ_i$ 的值，使得假设函数的直线最大程度的拟合我们的数据集

我们对所有样本进行求和，即对 i = 1 到 i = m (训练集的样本容量) 的样本，将对假设得到的预测值和实际值所得的差的平方进行相加得到总和。函数如下：

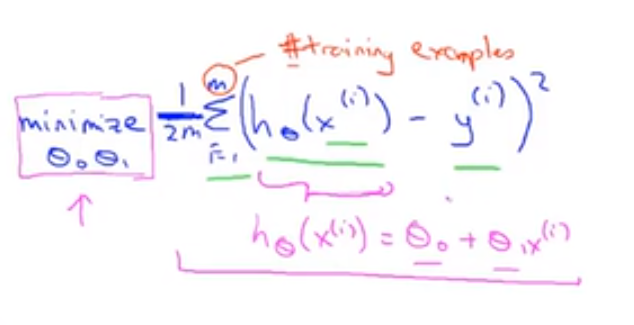
1/2m 是为了使得我们的数据更加直观，minimize θ0θ1 指关于 $θ_0$ 和 $θ_1$ 的最小化问题，即找到参数值 $θ_0$ 和 $θ_1$ 使得所有 $h_θ(x) - y$ 的平方和的 1/2m 尽可能的小。这便是线性回归的整体目标函数。

⭐⭐⭐ 代价函数：$J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$，其中 $h_θ(x) = θ_0 + θ_1x$

我们的目标便是选择出可以使得误差的平方和最小的模型参数 θ，即使得代价函数最小。

绘制一个等高线图，三个坐标分别为 $θ_0$ 和 $θ_1$ 和 $J(θ_0,θ_1)$：

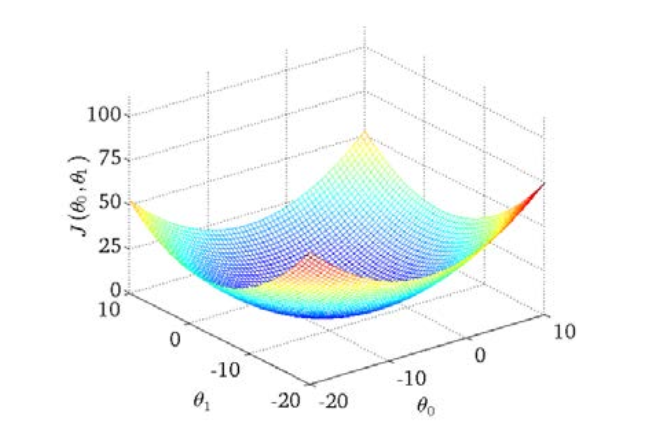
则可以看出在三维空间中存在一个使得 $J(θ_0,θ_1)$ 最小的点。

$J(θ_0,θ_1)$ 就是代价函数 cost function，也称为平方误差函数 squared error function，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

也许这个函数 $J(θ_0,θ_1)$ 有点抽象，可能你仍然不知道它的内涵，在接下来的几个视频里，我们要更进一步解释代价函数 J 的工作原理，并更直观地解释它在计算什么，以及我们使用它的目的。

三、代价函数的直观理解 Ⅰ

在上一节中，我们给出了代价函数一个数学上的定义。在这个视频里，让我们通过一些例子来获取一些直观的感受，看看代价函数到底是在干什么。

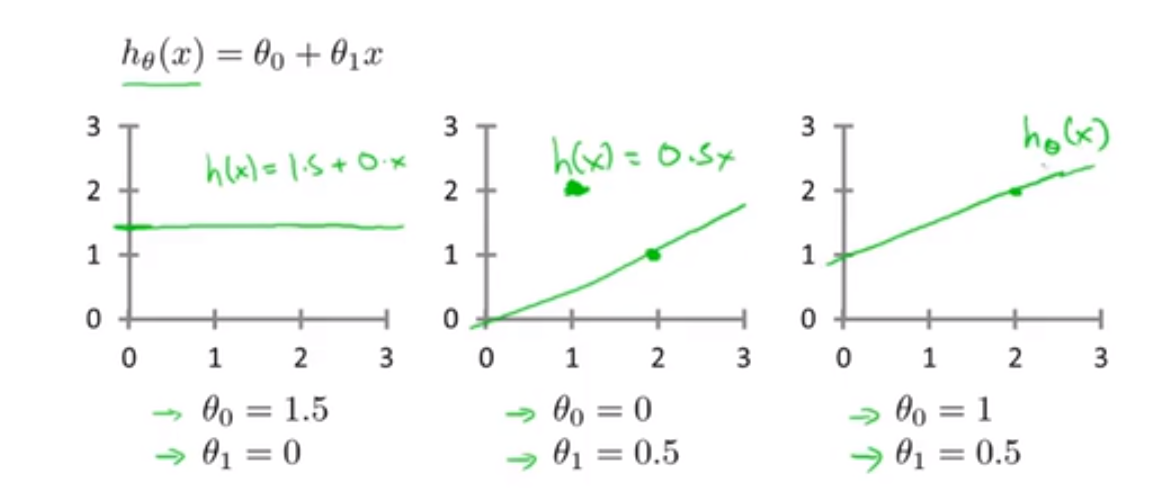
为了更好地使代价函数 J 可视化，我们使用一个简化的假设函数：$h_θ(x) = θ_1*x$，代价函数和之前相同。

基于上述简化的假设函数，我们来解释假设函数和代价函数之间的关系：

• 对于假设函数 h：它是关于 x 的函数

• 对于代价函数 J：它是关于 $θ_i1$ 的函数

每一个代价函数都对应一个假设函数，每一个不同的 θ1 ，我们都可以得到一个不同的 J(θ1) 的值

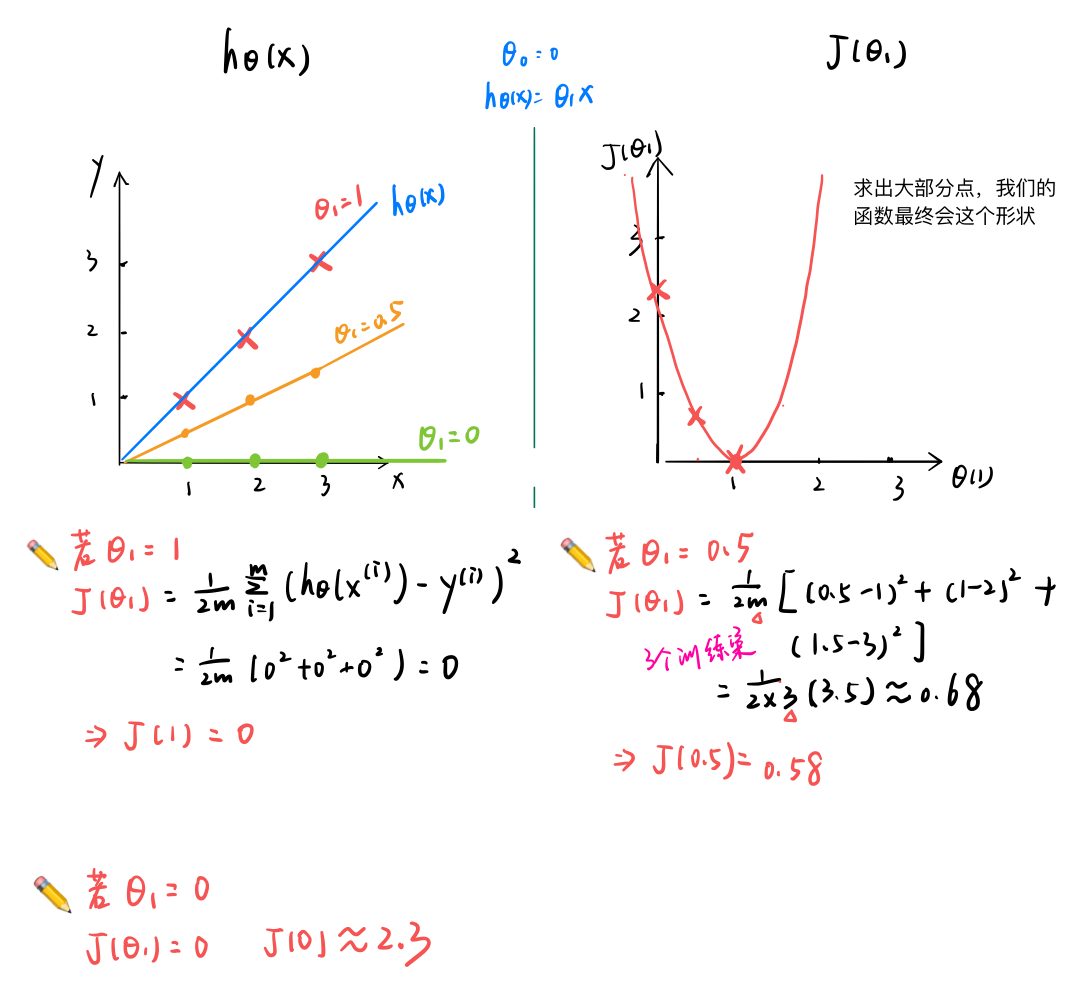
🎯 学习算法的优化目标，就是通过选择 θ1 的值，获得最小的 J(θ1) 。在上面的曲线中，当 θ1 = 1时，J(θ1) 最小，$h_{θ1}(x)$ 也确实是最佳匹配所有数据的直线。

下面我们将讨论带两个参数 θ0 和 θ1 时的图形

四、代价函数的直观理解 Ⅱ

我们保留全部参数 θ0 和 θ1 进行讨论：

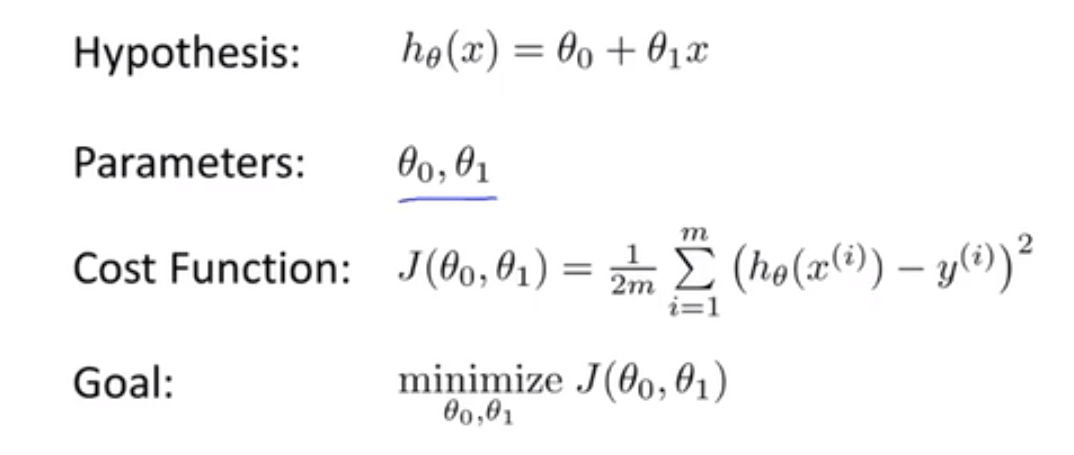
我们的代价函数图形最终会如下所示：

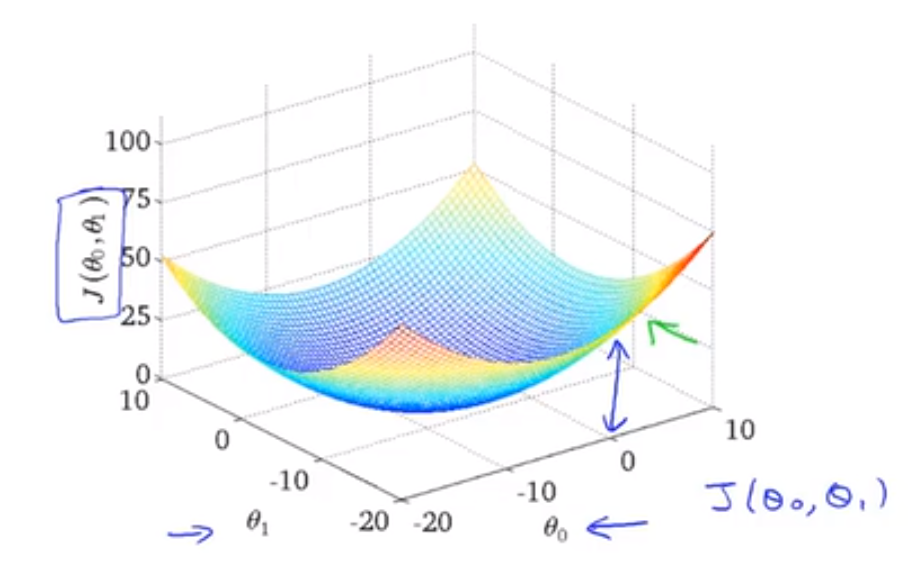
为了使这个图形显得直观，我们使用等高线图 contour plots 或者称为等高图像 contour figures 来表示，则可以看出在三维空间中存在一个使得 $J(θ_0,θ_1)$ 最小的点。

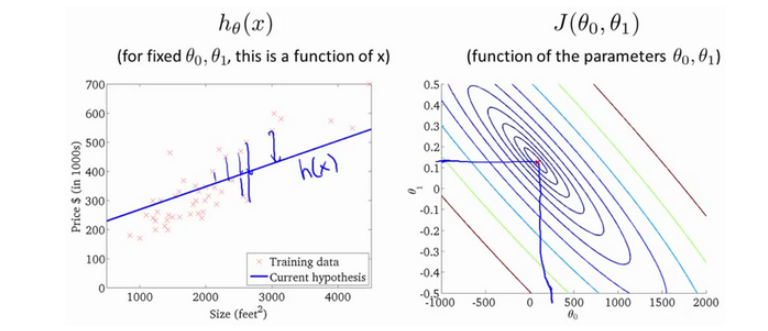
当然，我们真正需要的是一种有效的算法，能够自动地找出这些使代价函数取最小值的参数和。

我们也不希望编个程序把这些点画出来，然后人工的方法来读出这些点的数值，这很明显不是一个好办法。我们会遇到更复杂、更高维度、更多参数的情况，而这些情况是很难画出图的，因此更无法将其可视化，因此我们真正需要的是编写程序来找出这些最小化代价函数的 θ0 和 θ1 的值，在下一节中，我们将介绍一种算法，能够自动地找出能使代价函数 J 最小化的参数 θ0 和 θ1 的值。

五、梯度下降 Gradient descent

🔴 梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数 $J(θ_0,θ_1)$ 的最小值。

💡 梯度下降的思想 Outline：

• 首先随机选择一个参数的组合（θ0,θ1），计算代价函数

• 然后不断地改变参数组合的值，使得 J 的值减小，直到到达一个局部最小值（local minimum）。

  因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），🚩 选择不同的初始参数组合，可能会找到不同的局部最小值。

  
  

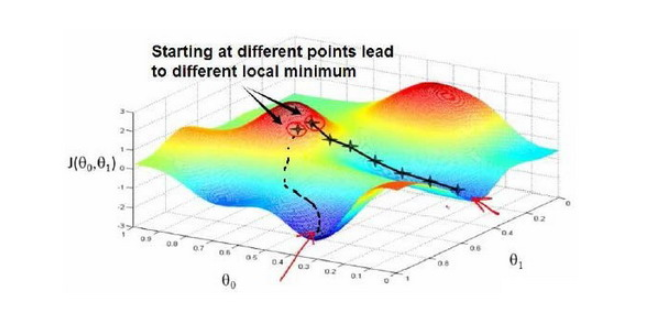
  💭 想象一下你正站立在山的这一点上，你看一下周围，你会发现最佳的下山方向，走了一步后，你再看看周围，然后再一次想想，我应该从什么方向下山？然后你按照自己的判断又迈出一步，重复上面的步骤，每到达一个新的点，都重新做决定从什么方向将会最快下山，然后又迈进了一小步，并依此类推，直到你接近局部最低点的位置。

  🔴 批量梯度下降（batch gradient descent）算法的公式为：

  
  

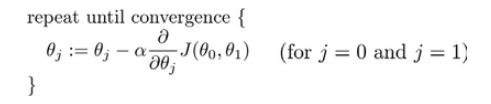
:= 这个符号表示赋值，这是一个赋值运算符 assignment operator

比如：a := b 表示将 b 的值赋给 a。

对于 = ，a = b 这是一个真假判定 truth assertion

其中 α 是学习率（learning rate），它决定了梯度下降时迈出的步子有多大。如果 α 很大，那么梯度下降就很迅速。在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

⭐⭐⭐ 在这个表达式中，如果你要更新这个等式，你需要同时更新 simultaneously update θ0 和 θ1：

θ0 := θ0 减去某项 ，并同时更新 θ1 := θ1 减去某项

实现方法是：应该先计算公式右边的部分并存储起来，通过那一部分计算出 θ0 和 θ1 的值，同时更新 θ0 和 θ1。

❌ 错误的做法：非同步更新，如果不同步更新，那么temp1 使用的 θ0 就是已经更新过的 θ0

同步更新是更自然的实现方法。当人们谈到梯度下降时，他们的意思就是同步更新。

在接下来的视频中，我们要进入批量梯度下降公式中的微分项 $α\frac{\partial}{\partial θ_j}J(θ_0,θ_1)$ 的细节之中

六、梯度下降的直观理解

对于微分项 $α\frac{\partial}{\partial θ_j}J(θ_0,θ_1)$，首先，我们来讲解偏导数 $\frac{\partial}{\partial θ_j}J(θ_0,θ_1)$ 的作用

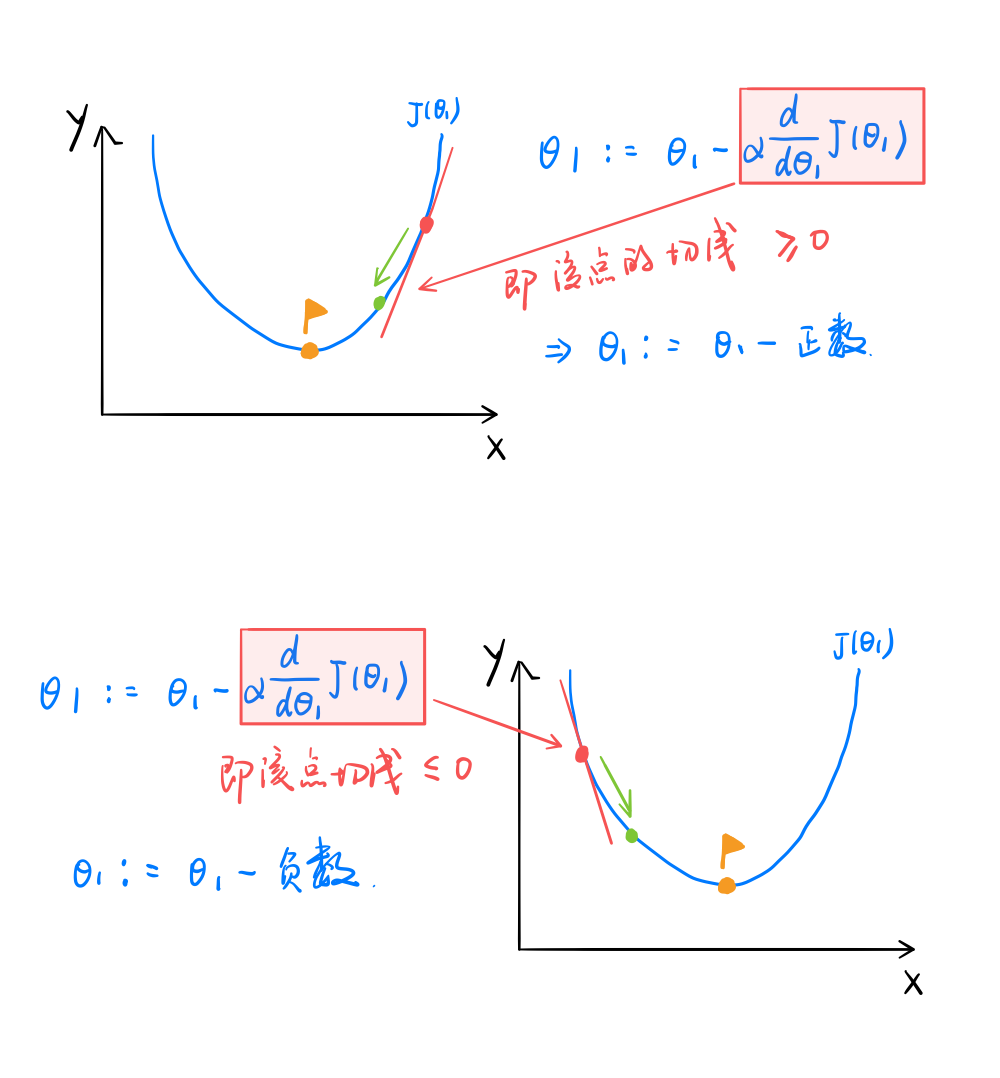
⭐ 显然，偏导数项的作用就是使得 J(θ1) 不断趋向于最小值，即控制梯度下降的方向

接下来，再解释一下学习速率 α

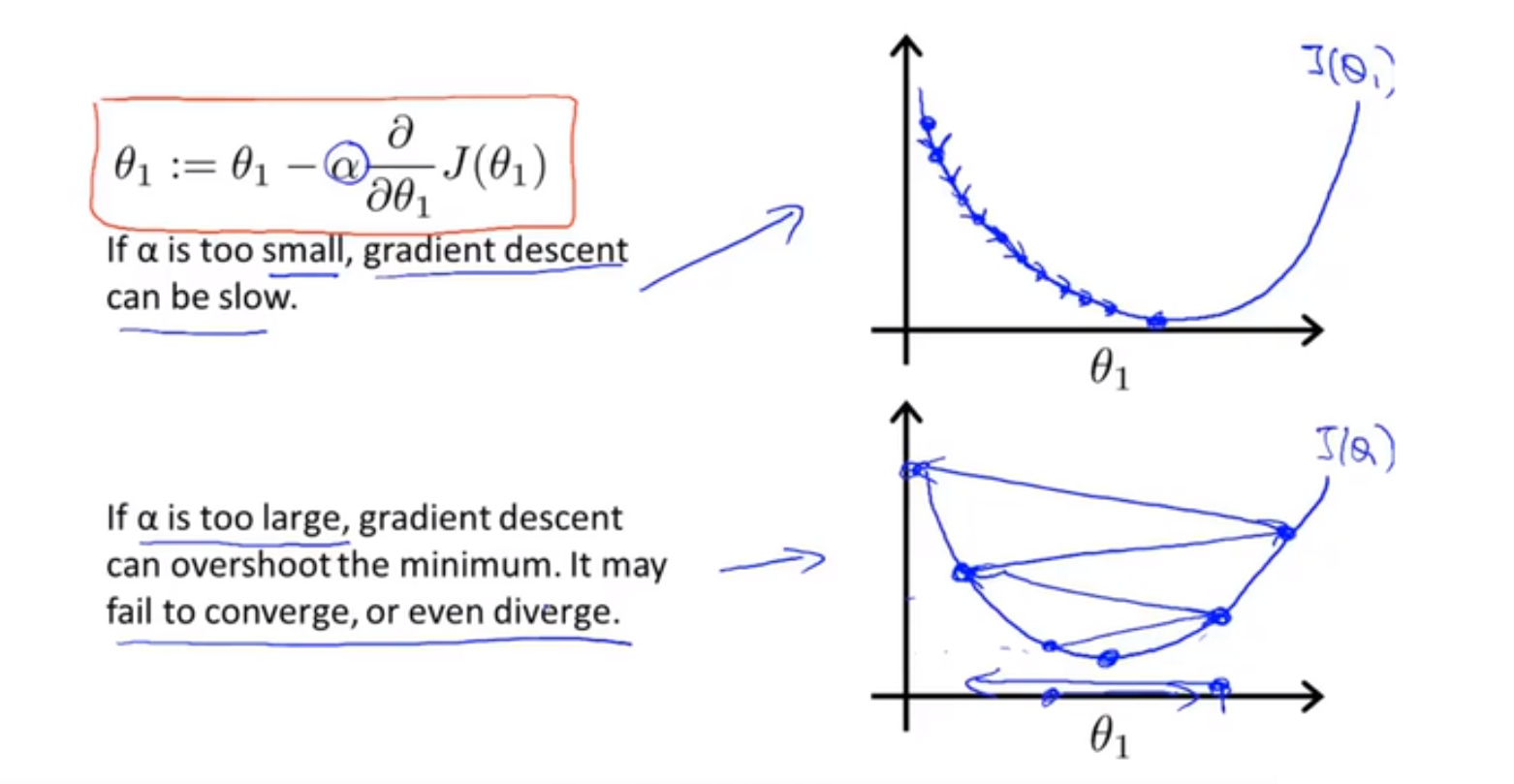
• If α is too small, gradient descent can be slow

• If α is too large, gradient descent can overshoot the minimum （越过最小值）. It may fail to converge（收敛）, or even diverge（发散）. 如果 α 太大，它会导致无法收敛，甚至发散

⭐ 显然，学习率 α 的作用就是控制梯度下降的速度

❓ 那么，如果我们预先把 θ1 放在一个局部的最低点，下一步梯度下降法会怎样工作？

假设你将 θ1 初始化在局部最低点，局部最优点的导数等于零。这意味梯度下降将不再有效，也就是新的 θ1 等于原来的 θ1 ，因此，如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即使学习速率 α 保持不变时，梯度下降也可以收敛到局部最低点。

我们来看一个例子，这是代价函数 J(θ)：

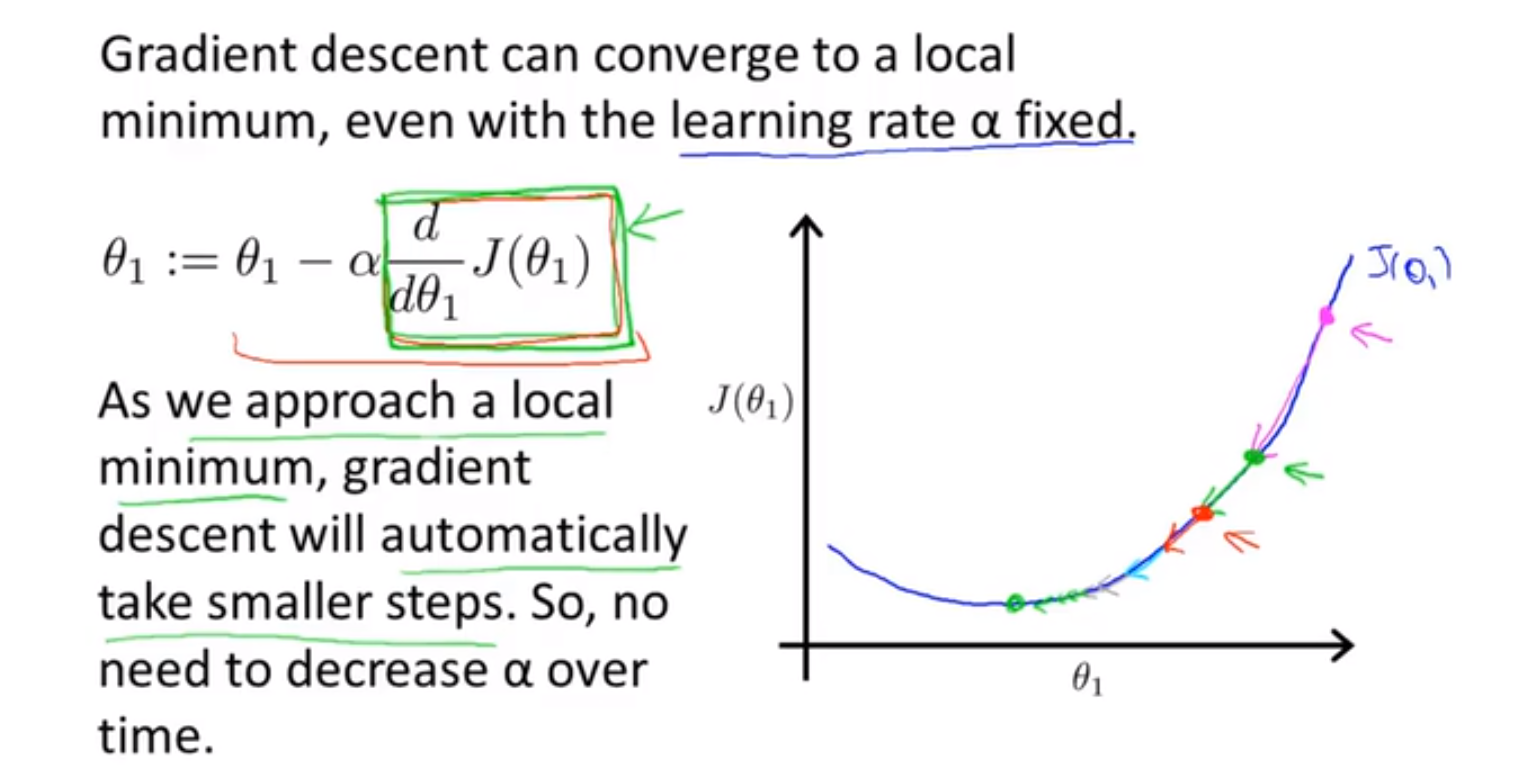
随着导数的越来越小，梯度下降的步伐也越来越小。

⭐ 在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小 α 。

这就是梯度下降算法，你可以用它来最小化任何代价函数 J，不只是线性回归中的代价函数 J。

🎉 接下来，结合梯度下降法以及平方代价函数，我们将得出第一个机器学习算法，即线性回归算法。

七、梯度下降的线性回归 Gradient descent for linear regression

推导过程：求出代价函数的偏导数

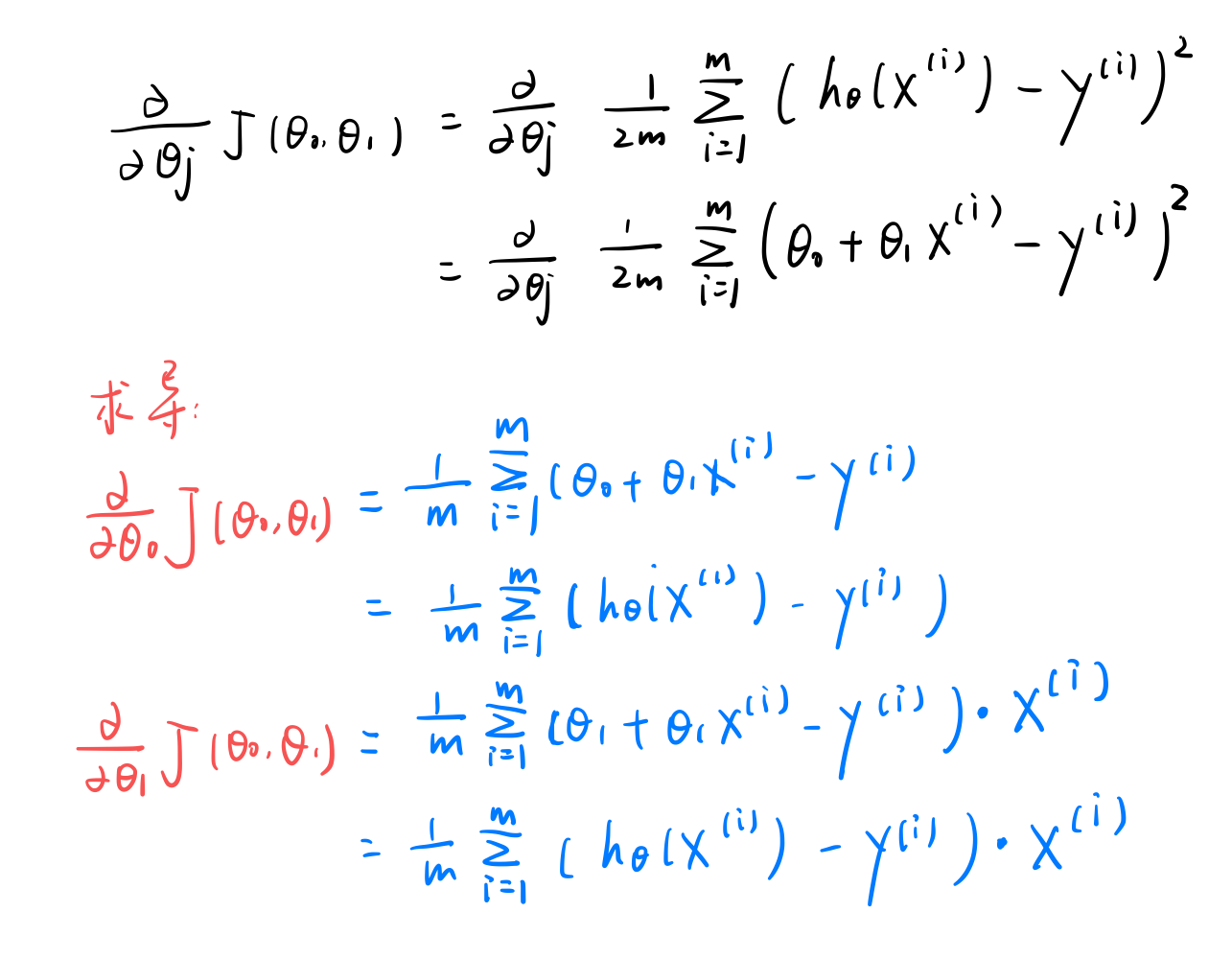
将我们求出的偏导数代入梯度下降算法：

下面我们通过一个动态图来直观感受梯度下降是如何影响代价函数的

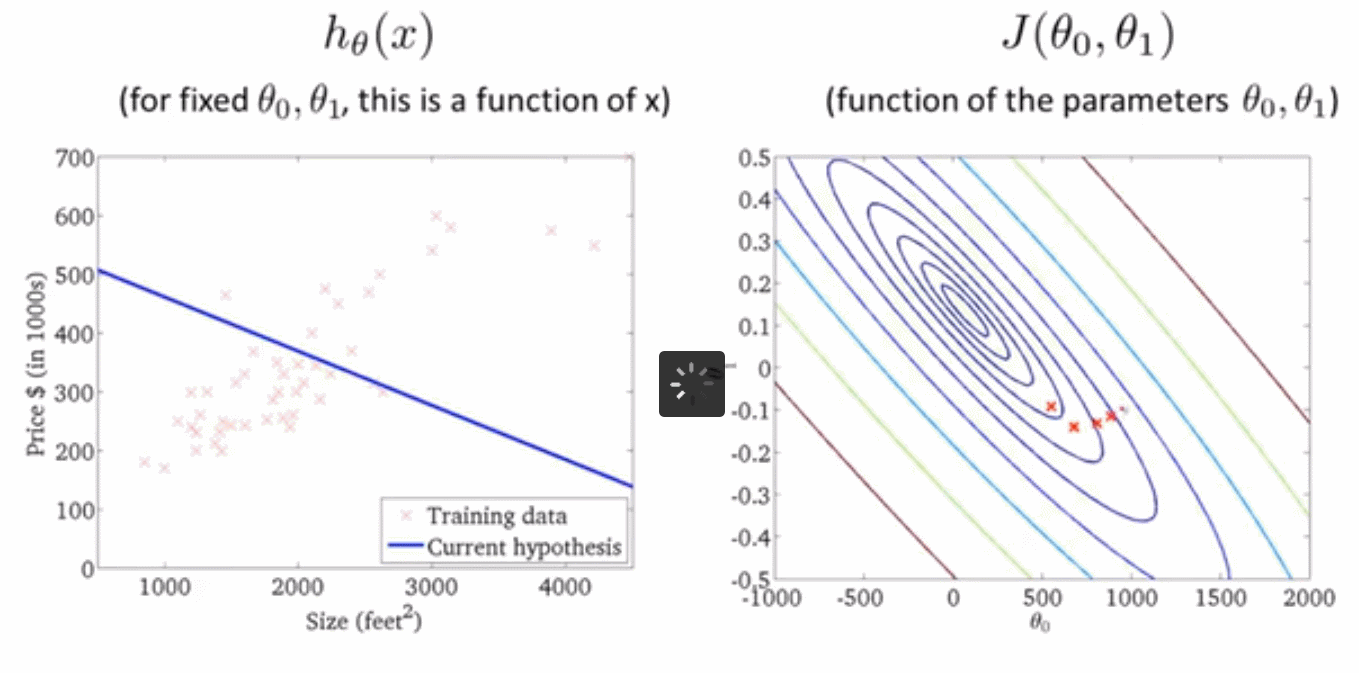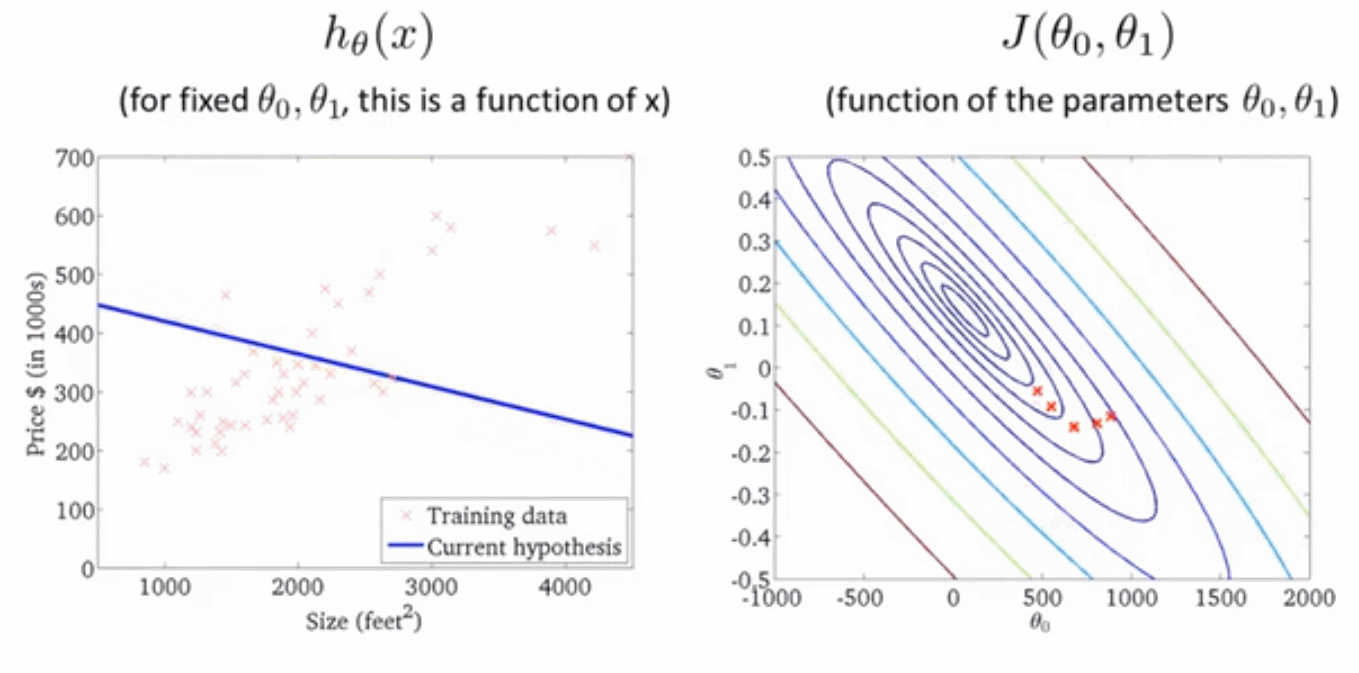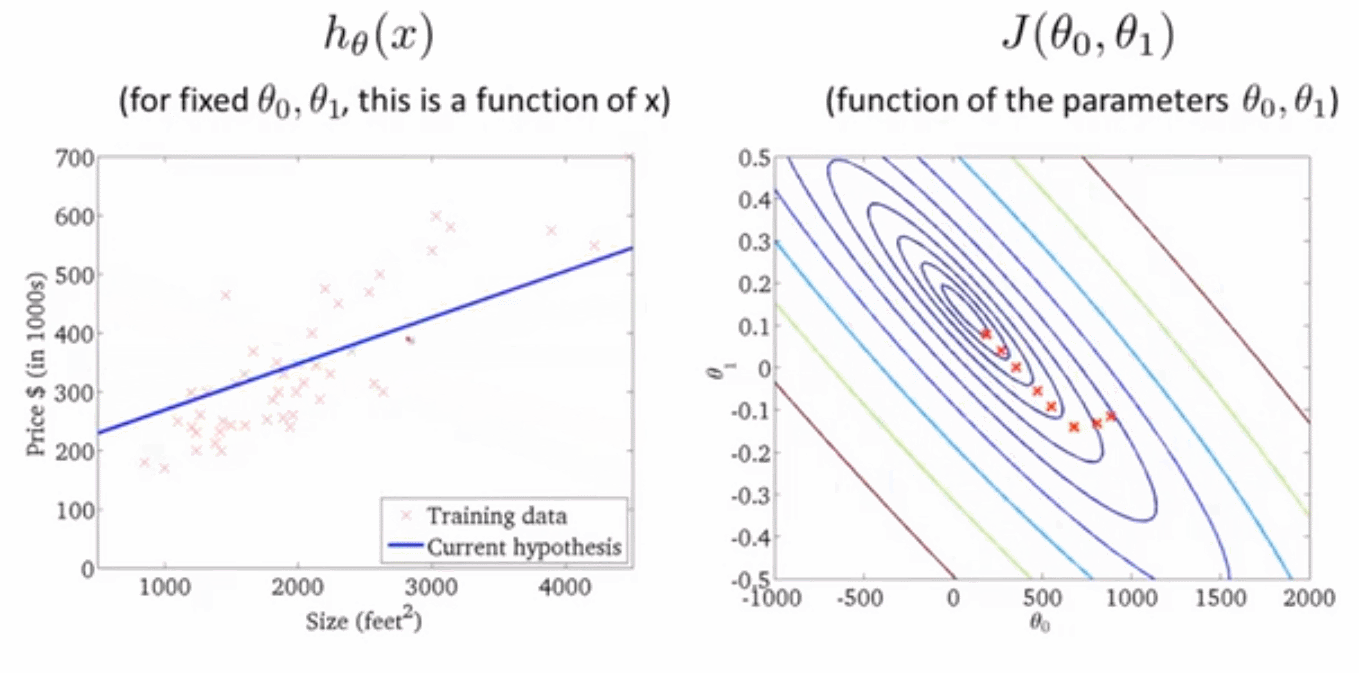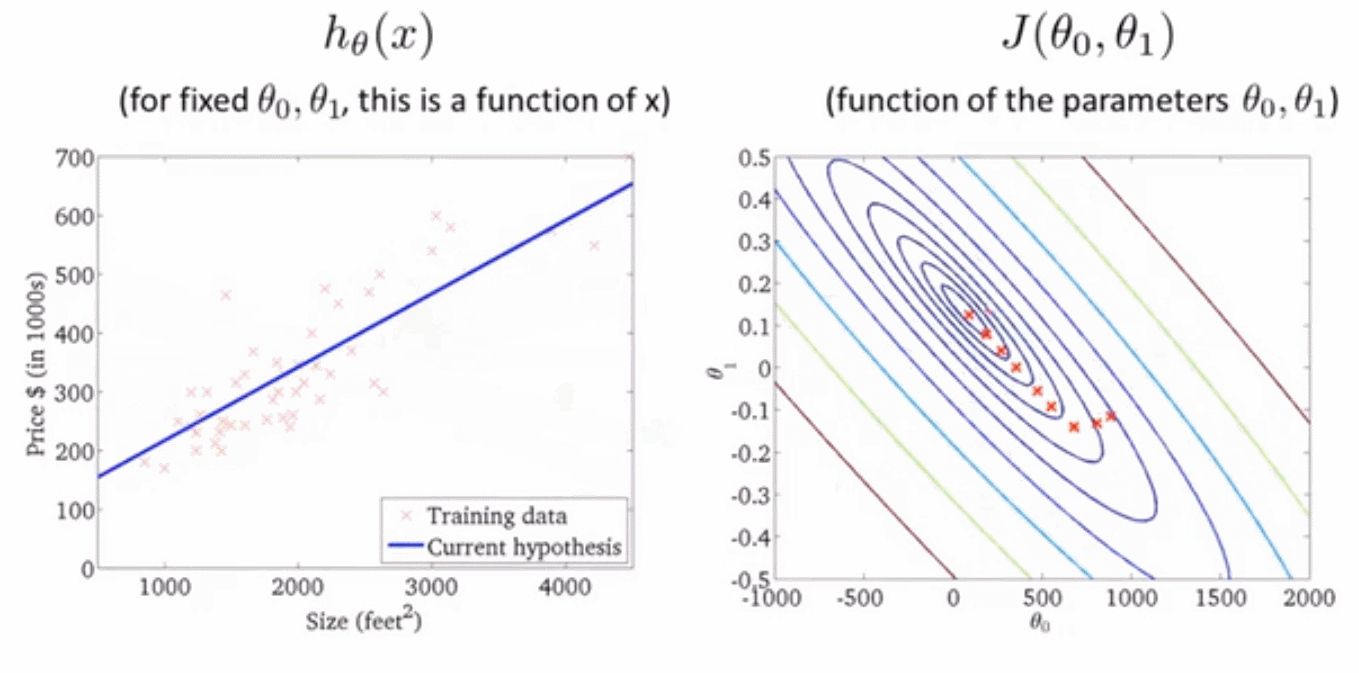
对于上述算法，我们也称为批量梯度下降 Batch Gradient descent 。" 批量" 指的是在梯度下降的每一步中，我们都用到了所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算。因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是每次只关注训练集中的一些小的子集。在后面的课程中，我们也将介绍这些方法。

现在我们已经掌握了梯度下降，我们可以在不同的环境中使用梯度下降法，我们还将在不同的机器学习问题中大量地使用它。所以，🎉 祝贺大家成功学会你的第一个机器学习算法。

✅ 总结一下 - 线性回归算法：

利用梯度下降算法自动的不断改变参数 θ 的值，当代价函数取得全局最小值时，假设函数就可以最大程度地拟合我们的数据集。

在接下来的课程中，我们将学习泛化的梯度下降算法，这将使梯度下降更加强大。

⭐ 小结

总结一下单变量线性回归的知识点：

• 假设函数：预测 y 关于 x 的直线 - $h_θ(x) = θ_0 + θ_1*x$

• 代价函数：当代价函数取得最小值时（取决于 θ），假设函数将最佳拟合数据集 - $J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$

• （批量）梯度下降：使用梯度下降算法来求出代价函数 $J(θ_0,θ_1)$ 的最小值 -
  

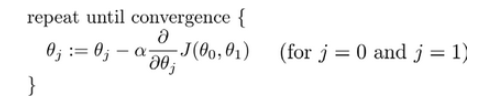
✍ Quiz

① 第 1 题

Consider the problem of predicting how well a student does in her second year of college/university, given how well she did in her first year.

Specifically, let x be equal to the number of "A" grades (including A-. A and A+ grades) that a student receives in their first year of college (freshmen year). We would like to predict the value of y, which we define as the number of "A" grades they get in their second year (sophomore year).

Refer to the following training set of a small sample of different students' performances (note that this training set may also be referenced in other questions in this quiz). Here each row is one training example. Recall that in linear regression, our hypothesis is hθ(x)=θ0+θ1x, and we use m to denote the number of training examples.

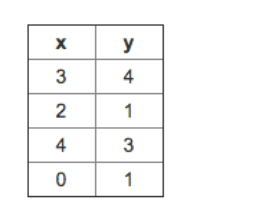
For the training set given above, what is the value of m? 对于上面给出的训练集，m的值是多少？

• ✅ m = 4

② 第 2 题

for this question, assume that we are using the training set from Q1. Recall our definition of the cost function was $J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$

What is J(0, 1) ?

对于这个问题，假设我们使用第一题中的训练集。并且，我们对代价函数的定义是 $J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$ ，求 J(0,1)

• ✅ 已知 hθ(x)=θ0+θ1x，$J(\theta_0,\theta_1)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2$

  
  

  θ0 = 0，θ1 = 1，代入即可：

  $J(0,1)=\frac{1}{2*4}\left((3-2)^2+(1-2)^2+(0-1)^2+(4-3)^2 \right)=0.5$

③ 第 3 题

Suppose we set $\theta_0 = -1$, $\theta_1 = 0.5$ . What is $h_{\theta}(4)$ ?

• ✅ $h_{\theta}(4)=-1+0.5*4=1$

④ 第 4 题

In the given figure, the cost function $ J(\theta_0,\theta_1)$ has been plotted against $\theta_0$ and $\theta_1$, as shown in 'Plot 2'. The contour plot for the same cost function is given in 'Plot 1'. Based on the figure, choose the correct options (check all that apply). 代价函数J(θ0,θ1)与θ0,θ1的关系如图2所示。“图1”中给出了相同代价函数的等高线图。根据图示，选择正确的选项（选出所有正确项）

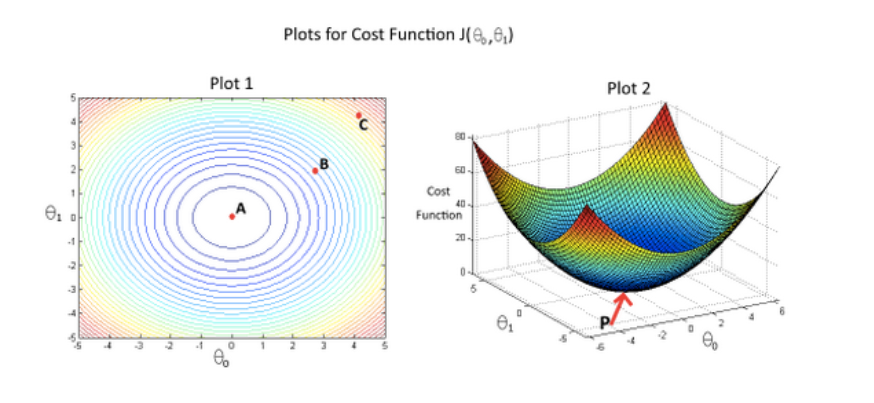
• If we start from point B, gradient descent with a well-chosen learning rate will eventually help us reach at or near point A, as the value of cost function $J(\theta_0,\theta_1$) is maximum at point A. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近A点，即代价函数J(θ0,θ1)在A点有最大值

• ✅ Point P (the global minimum of plot 2) corresponds to point A of Plot 1. 点P（图2的全局最小值）对应于图1的点A

• Point P (The global minimum of plot 2) corresponds to point C of Plot 1. 点P（图2的全局最小值）对应于图1的点C

• ✅ If we start from point B, gradient descent with a well-chosen learning rate will eventually help us reach at or near point A, as the value of cost function $J(\theta_0,\theta_1)$ is minimum at A. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近A点，即代价函数J(θ0,θ1)在A点有最小值

• If we start from point B, gradient descent with a well-chosen learning rate will eventually help us reach at or near point C, as the value of cost function $J(\theta_0,\theta_1)$ is minimum at point C. 从B点开始，学习率合适的梯度下降算法会最终帮助我们到达或者接近C点，即代价函数J(θ0,θ1)在C点有最小值

⑤ 第 5 题

Suppose that for some linear regression problem (say, predicting housing prices as in the lecture), we have some training set, and for our training set we managed to find some $\theta_0, \theta_1 $such that$ J(\theta_0, \theta_1)=0$.

Which of the statements below must then be true? (Check all that apply.)

假设对于某个线性回归问题（比如预测房价），我们有一些训练集，对于我们的训练集，我们能够找到一些θ0,θ1，使得J(θ0,θ1)=0。 以下哪项陈述是正确的？（选出所有正确项）

• 为了实现这一点，我们必须有θ0=0,θ1=0，这样才能使J(θ0,θ1)=0

• ✅ 对于满足$J(θ_0,θ_1)=0$ 的θ0,θ1的值，其对于每个训练例子$(x^{(i)},y^{(i)})$，都有$h_θ(x^{(i)})=y^{(i)}$

• 这是不可能的：通过J(θ0,θ1)=0的定义，不可能存在θ0,θ1使得J(θ0,θ1)=0

• 即使对于我们还没有看到的新例子，我们也可以完美地预测y的值（例如，我们可以完美地预测我们尚未见过的新房的价格）

🍟 多变量线性回归 Linear Regression with Multiple Variables

一、多维特征 Multiple Features

目前为止，我们探讨了单变量/特征的回归模型，现在我们对房价模型增加更多的特征，例如房间数、楼层等，构成一个含有多个变量的模型，模型中的特征为 $(x1,x2,x3...xn)$ 。

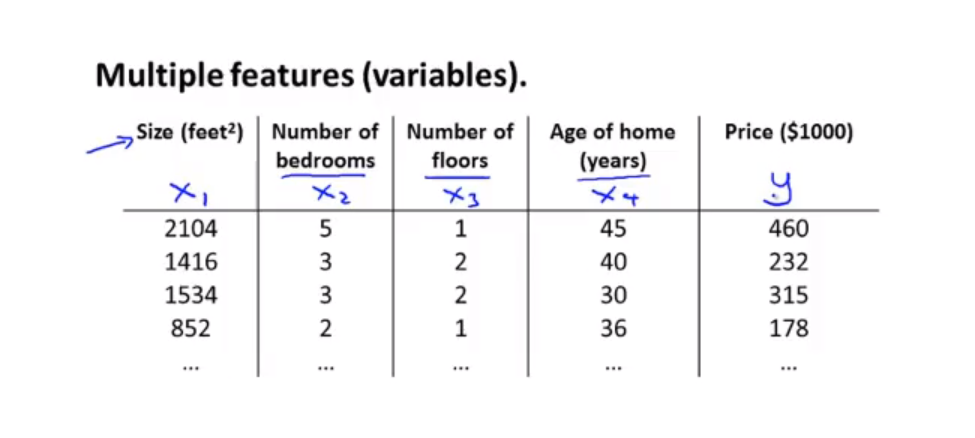
增添更多特征后，我们引入一系列新的注释：

• n 代表特征的数量

  如上图 n = 4

• $x^{(i)}$ 代表第 i 个训练实例，即特征矩阵中的第 i 行，是一个向量（vector）

  比如上图的 $x^{(2)} = \begin{bmatrix} 1416 \ 3 \ 2 \ 40 \ 232\end{bmatrix}$

• $x^{(i)}_j$ 代表特征矩阵中第 i 行的第 j 个特征，也就是第 i 个训练实例的第 j 个特征

  比如上图的 $x^{(2)}_2$ = 3 ，$x^{(2)}_3$ = 2

支持多变量的假设 表示为：$h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $

这个公式中有个参数和个变量，为了使得公式能够简化一些，引入 x0 = 1，则公式转化为：

⭐ $h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $

➡ $x = \begin{bmatrix} x_0 \ x_1 \ x_2 \ ... \ x_n\end{bmatrix}$，$θ = \begin{bmatrix} θ_0 \ θ_1 \ θ_2 \ ... \ θ_n\end{bmatrix}$，此时模型中的参数是一个 n+1 维的向量，任何一个训练实例也都是 n+1 维的向量

⭐ $h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $ = $\begin{bmatrix} θ_0 & θ_1 & θ_2 & ... & θ_n\end{bmatrix}$ $\begin{bmatrix} x_0 \ x_1 \ x_2 \ ... \ x_n\end{bmatrix}$ = $θ^Tx$

二、多变量梯度下降 Gradient Descent for Multiple Variables

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：$J(θ_0,θ_1,...θ_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$ ，

其中：$h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $ = $θ^Tx$ （x0 = 1）

我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。 多变量线性回归的批量梯度下降算法为：

💬 代码示例：

$J(θ_0,θ_1,...θ_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$ ，

其中：$h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $ = $θ^Tx$

Python 代码：

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

三、梯度下降法实践1-特征缩放 Gradient Descent in Practice I - Feature Scaling

在我们面对多维特征问题的时候，我们要保证这些特征都在小范围内波动，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到 -1 到 +1 之间。这样我们的梯度下降算法将会更快的收敛 converge much faster ，如图：

🔴 Feature Scaling：Get every feature into approximately a -1 ≤ xi ≤ 1 range.

接近 （-1，1）的范围，不过大或者过小，都可以认为是合理的范围

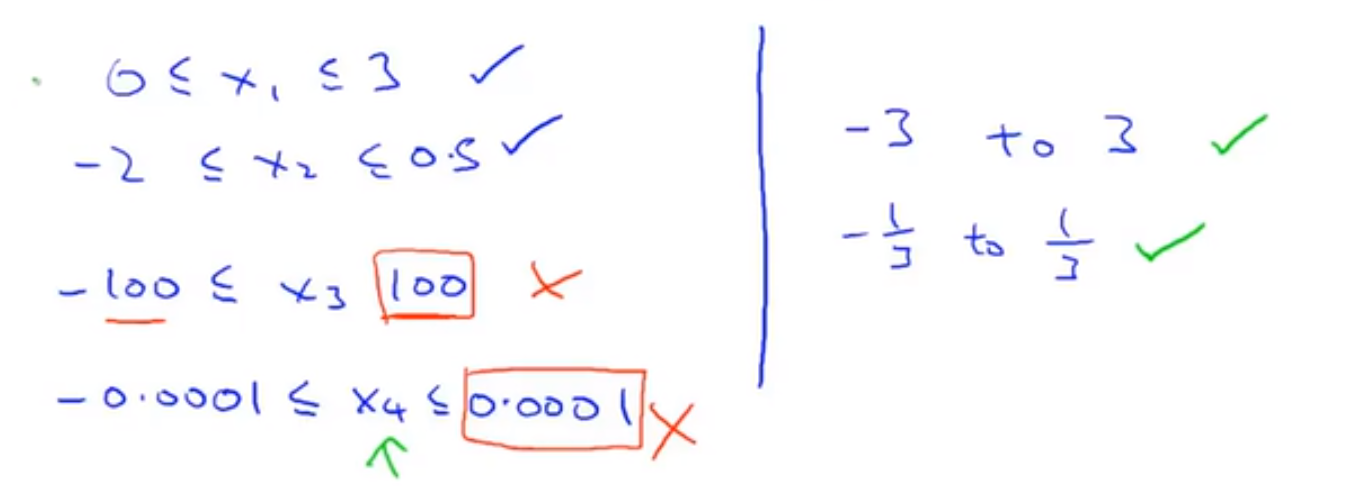
⭐ Mean normalization 均值归一化：Replace xi with xi - μi to make features have approximately zero mean (Do not apply to x0 = 1)

最简单的缩小特征值的方法就是均值归一化：令 $x_n = \frac{x_n - μ_n}c$，其中 $μ_n$ 是平均值，$s_n$ 是标准差

🚩 总结：通过使用特征缩放这个简单的方法就可以使得梯度下降的速度变快，收敛所需的迭代次数更少

四、梯度下降法实践2-学习率 Gradient Descent in Practice II - Learning Rate

❓ How to make sure gradient descent is working correctly

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

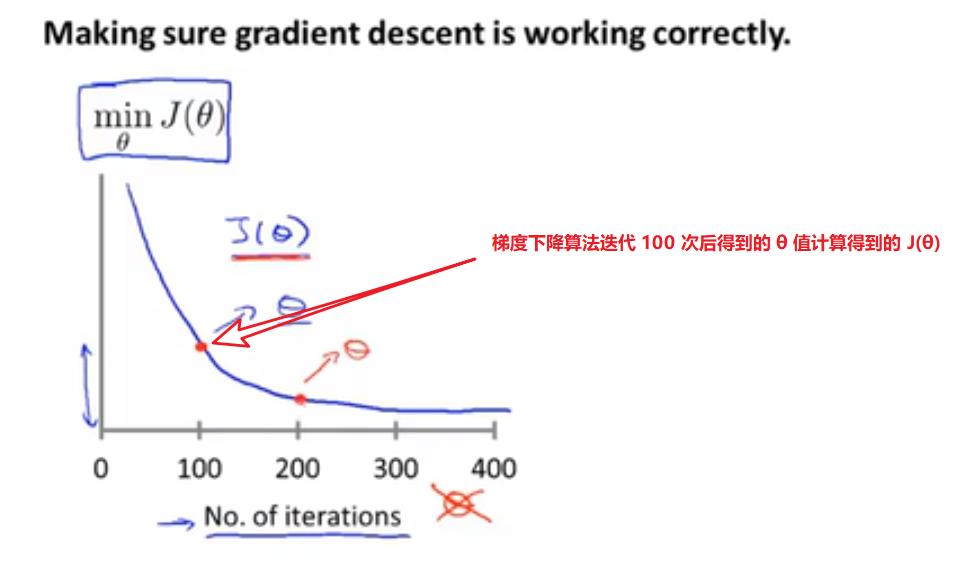
如果梯度下降是正确的话，那么每次迭代后代价函数都会减小。不同的情况代价函数趋向于收敛所需要的迭代次数也各不相同

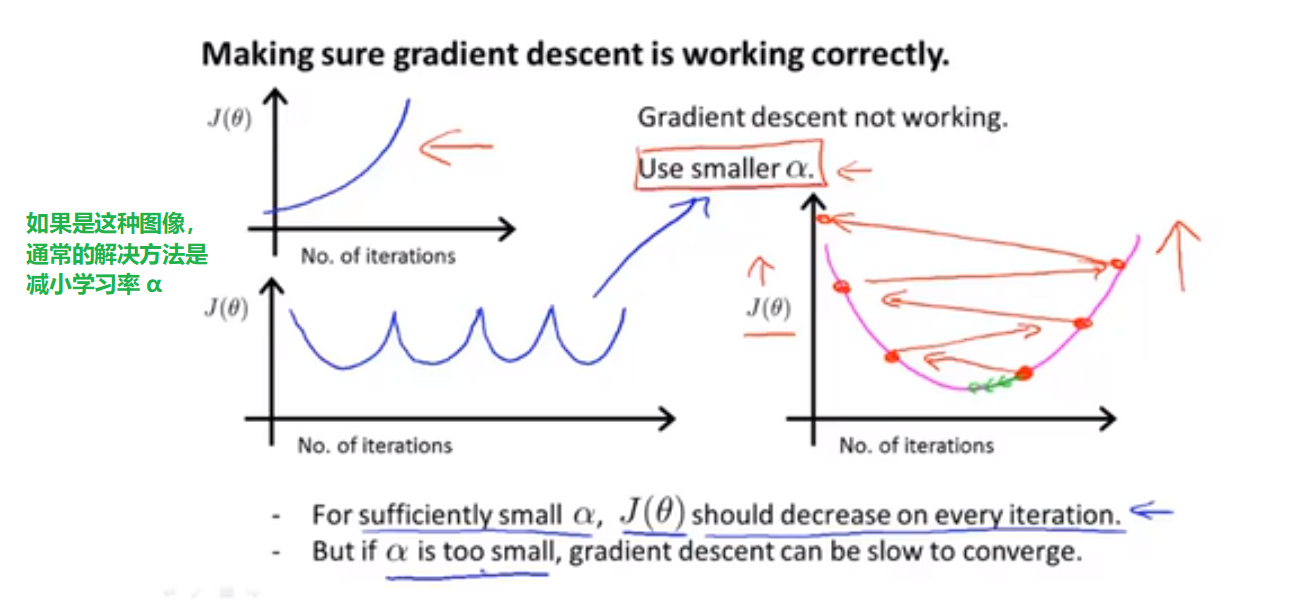
❓ How to choose learning rate α

梯度下降算法的每次迭代受到学习率的影响：

• 如果学习率 α 过小，则达到收敛所需的迭代次数会非常高；

• 如果学习率 α 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。

通常可以考虑尝试些学习率：α = 0.01，0.03，0.1，0.3，1，3，10（每隔10倍取值）

五、特征和多项式回归 Features and Polynomial Regression

多项式回归使得我们能够使用线性回归的方法来拟合非常复杂的函数，甚至是非线性函数。

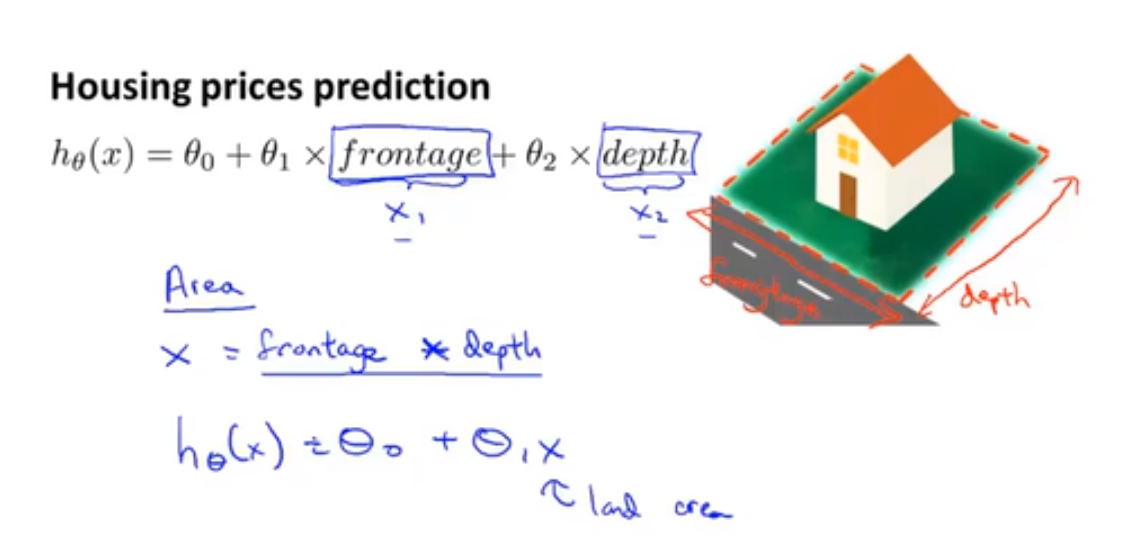
💬 以房价预测问题为例，假设我们拥有两个特征：拥有的土地的宽度 frontage 以及 房子的深度 depth

$h_θ(x) = θ_0 + θ_1 * frontage + θ_2 * depth$

其实我们可以自己创造特征 define new features：比如 特征 area (面积) = frontage x depth，则 $h_θ(x) = θ_0 + θ_1 * area$

线性回归并不适用于所有数据，有时我们需要曲线来适应我们的数据，比如一个二次方模型，其中：$h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2^2$ 或者三次方模型： $h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2^2 + θ_3x_3^3$

二次函数可能并不是最好的模型，因为二次函数曲线会下降，我们可以选择采用三次函数模型：

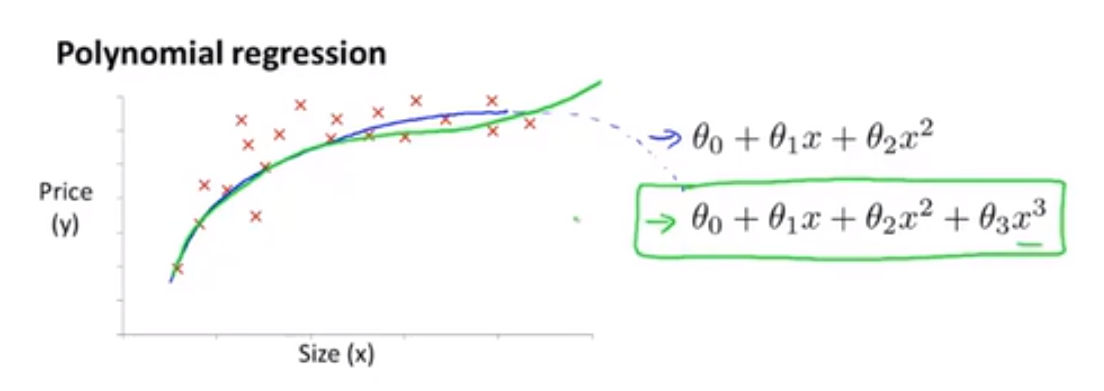
我们可以令： $x_2 = x_2^2, x3 = x_3^3$，从而将模型转化为线性回归模型，如下：

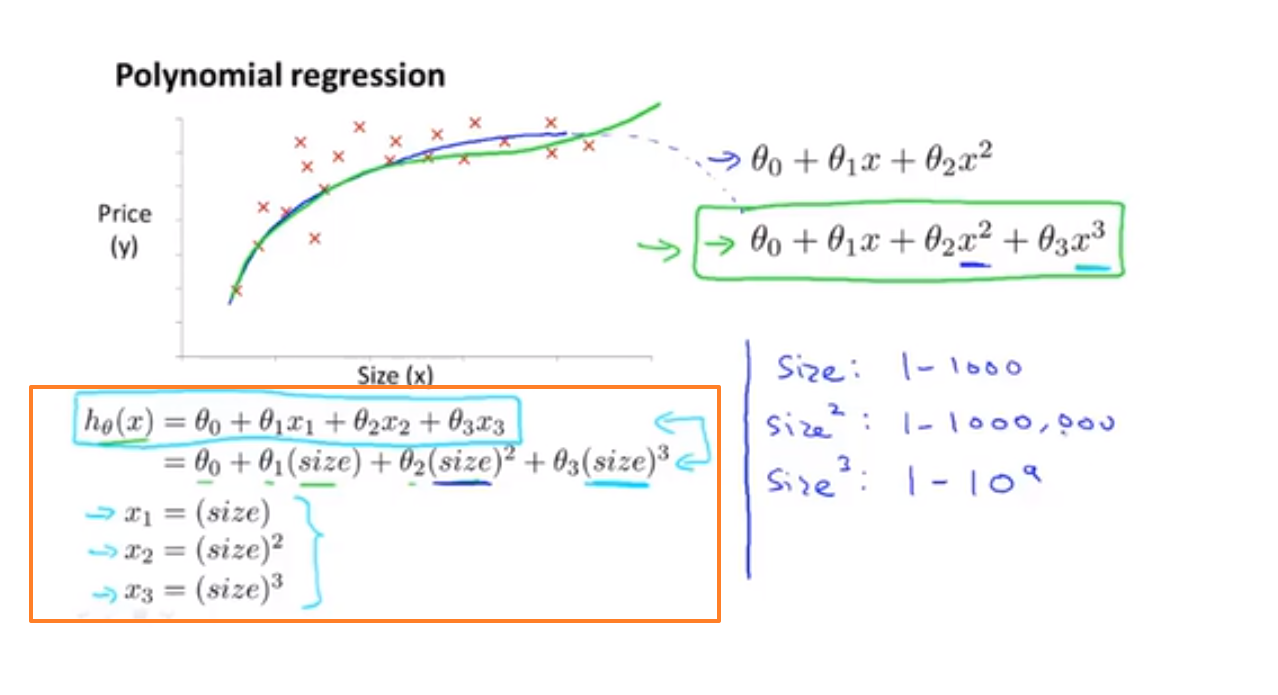
🚨 显然：如果我们采用多项式回归模型，在运行梯度下降算法前，特征缩放非常有必要。

特征的抉择可能有点困难，有这么多不同的特征，我们到底该决定使用什么特征，在之后的课程中，我们会学习一些算法，它们能够自动选择要使用什么特征，因此，我们可以让算法观察给出的数据，并自动选择，到底该选择一个二次函数，三次函数还是其他别的函数

🚩 OK，本节我们需要知道的就是我们可以自由选择使用什么特征，并且通过设计不同的特征，我们能够用更复杂的函数拟合数据，而不是只用一条直线去拟合

六、正规方程 Normal Equation (区别于迭代方法的直接解法)

💡 到目前为止，我们都在使用梯度下降算法（经过很多次迭代来收敛到全局最小值），但是对于某些线性回归问题，正规方程方法是更好的解决方案。

🔴 Normal equation：Method to solve fro θ analytically 一次性求出参数 θ 的最优值

💬 举个例子来解释一下：

假设我们有一个代价函数 $J(θ) = aθ^2 + bθ + c，θ ∈ R$

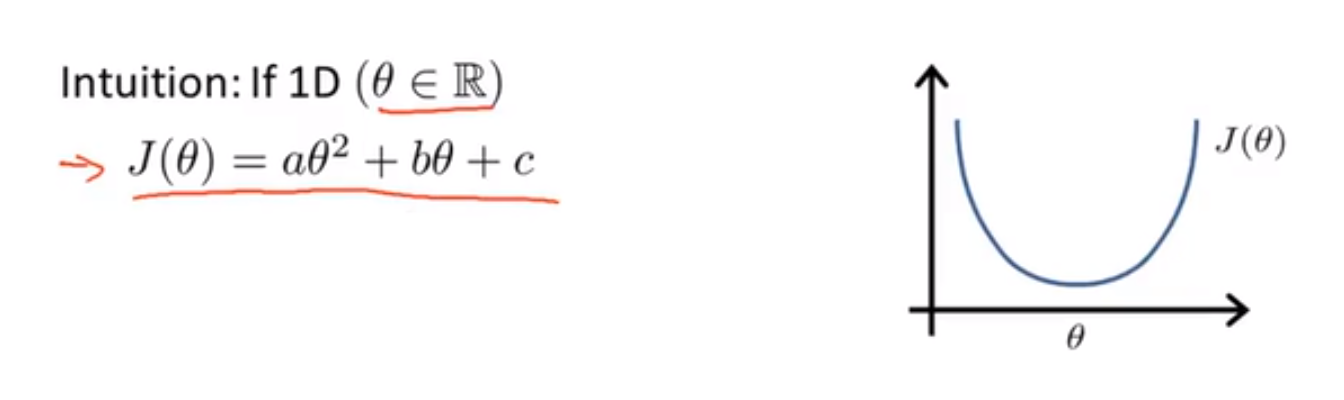
当 θ 为实数 real number的时候，我们获取该二次函数的最小值（最小化该函数）的方法就是对其进行求导并将导数置零，求得 θ 的值并带入 J(θ) 即可求得 J(θ) 的最小值

如果 θ 不是实数，而是一个 n+1 维的参数向量，而代价函数是 $J(θ_0,θ_1,...θ_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^(i)) - y^(i))^2$ ，我们最小化这个代价函数 J 的方法就是逐个对参数 $θ_i$ 求 J 的偏导数，并将它们全部置零。显然，这是非常麻烦的。🔵 运用正规方程方法 $θ = (X^TX)^{-1}X^Ty$ 求解参数 θ 举例如下：

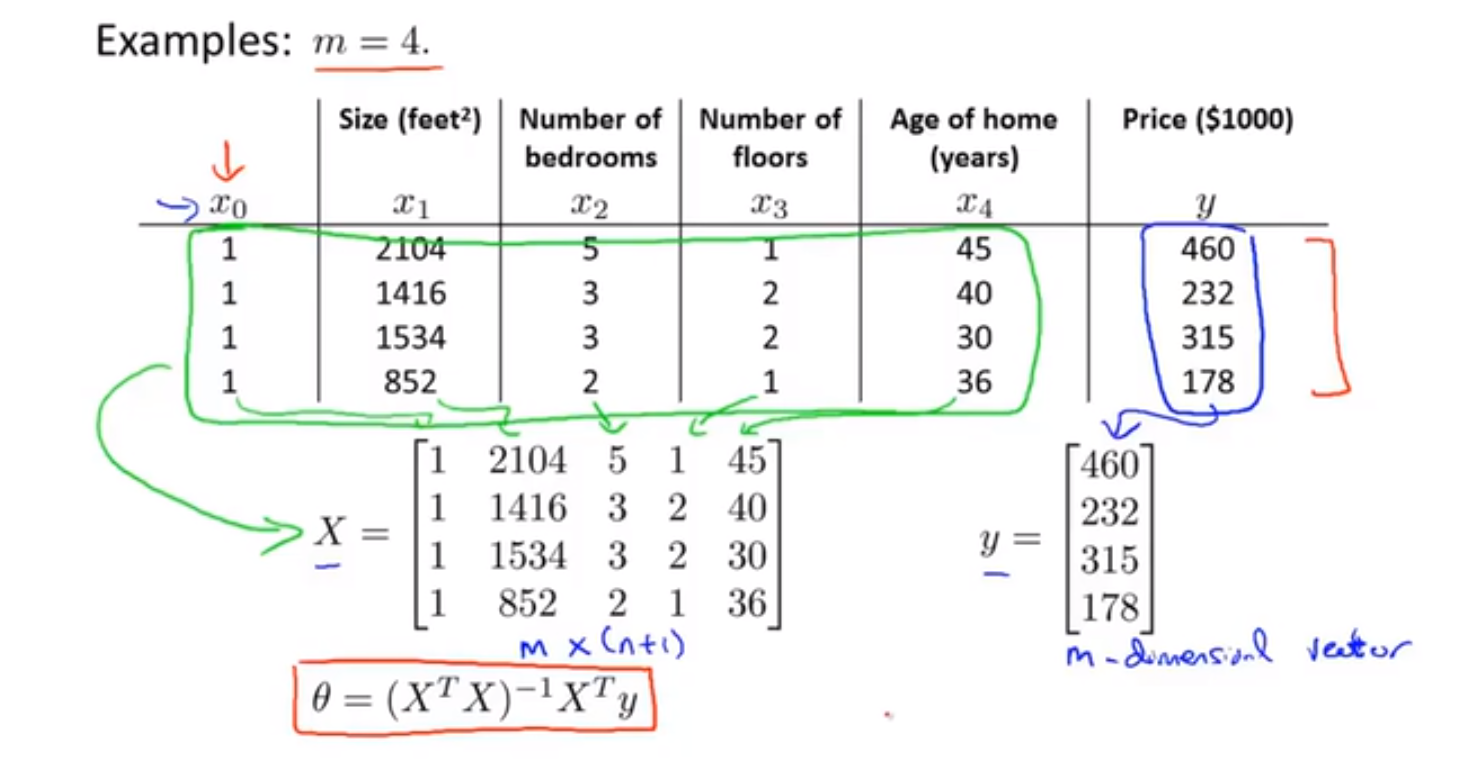
注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。

在 Octave 中，正规方程写作：

pinv(X'*X)*X'*y

正规方程的python实现：

import numpy as np

def normalEqn(X, y):
    # X.T@X等价于X.T.dot(X)
    theta = np.linalg.inv(X.T@X)@X.T@y  # nplinalg.inv 求逆
    return theta

🚨 如果你采用正规方程，那么就不需要特征缩放

⭐ 梯度下降与正规方程的比较：

👍 总结一下，只要特征变量的数目并不大，正规方程是一个很好的计算参数的替代方法。具体地说，只要特征变量数量小于一万，我通常使用正规方程法，而不使用梯度下降法。

随着我们要讲的学习算法越来越复杂，例如，当我们讲到分类算法，像逻辑回归算法，我们会看到，实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为正规方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，正规方程法是一个比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。

⭐ 小结

回顾一下单变量线性回归的知识点：

• 假设函数：预测 y 关于 x 的直线 - $h_θ(x) = θ_0 + θ_1*x$

• 代价函数：当代价函数取得最小值时（取决于 θ），假设函数将最佳拟合数据集 - $J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$

• （批量）梯度下降：使用梯度下降算法来求出代价函数 $J(θ_0,θ_1)$ 的最小值 -
  

总结一下多变量线性回归的知识点：

• 假设函数：预测 y 关于 x 的曲线 - $h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n （x_0 = 1）$ = $\begin{bmatrix} θ_0 & θ_1 & θ_2 & ... & θ_n\end{bmatrix}$ $\begin{bmatrix} x_0 \ x_1 \ x_2 \ ... \ x_n\end{bmatrix}$ = $θ^Tx$

• 代价函数：当代价函数取得最小值时（取决于 θ），假设函数将最佳拟合数据集 - $J(θ_0,θ_1,...θ_n) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$

• （批量）梯度下降：使用梯度下降算法来求出代价函数 $J(θ_0,θ_1)$ 的最小值 -
  

  如果梯度下降是正确的话，那么每次迭代后代价函数都会减小

• 特征缩放：在我们面对多维特征问题的时候，我们要保证这些特征都在小范围内波动（-1 ~ 1 之间），这将帮助梯度下降算法更快地收敛。最简单的缩小特征值的方法就是均值归一化：令 $x_n = \frac{x_n - μ_n}c$，其中 $μ_n$ 是平均值，$s_n$ 是标准差

• 学习率 α：梯度下降算法的每次迭代受到学习率的影响：

  • 如果学习率 α 过小，则达到收敛所需的迭代次数会非常高；

  • 如果学习率 α 过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛

• 正规方程：一次性求出参数 θ 的最优值 - $θ = (X^TX)^{-1}X^Ty$

✍ Quiz

① 第 1 题

假设 m = 4 个学生上了一节课，有期中考试和期末考试。你已经收集了他们在两次考试中的分数数据集，如下所示：

你想用多项式回归来预测一个学生的期中考试成绩。具体地说，假设你想拟合一个 hθ(x)=θ0+θ1x1+θ2x2 的模型，其中 x1 是期中得分，x2 是（期中得分）^2。此外，你计划同时使用特征缩放（除以特征的 “最大值 - 最小值” 或范围）和均值归一化。

标准化后的$x_2^{(4)}$特征值是多少？（提示：期中 = 89，期末 = 96是训练示例1）

• ✅ 均值归一化：$x_2^{(4)} = \frac{x_2^{(4)} - μ_2}{s_2}$，

  $μ_2$ 表示 平均值 = $\frac{x_2^{1} + x_2^{2} + x_2^{3} + x_2^{4}}{4} = \frac{7921+5184+8835+4761}{4} = 6675.5$，

  $s_2$ 表示标准差 = max - min = 8836 - 4761 = 4075，得出 $x_2^{(4)} = \frac{4761 - 6675.5}{4075} ≈ -0.47$

② 第 2 题

用 α = 0.3 进行 15 次梯度下降迭代，每次迭代后计算 J(θ)。你会发现 J(θ) 的值下降缓慢，并且在 15 次迭代后仍在下降。基于此，以下哪个结论似乎最可信？

• α = 0.3 是学习率的有效选择

• 与其使用 α 当前值，不如尝试更小的 α 值（比如α = 0.1）

• ✅ 与其使用 α 当前值，不如尝试更大的 α 值（比如α = 1.0）

  迭代 15 次后迭代下降速度缓慢，那么 α=0.3 自然不是合适的值，需要调大一些才好。

③ 第 3 题

假设您有 m = 14 个训练示例，有 n = 3 个特征（不包括需要另外添加的恒为 1 的截距项 $x_0$），正规方程是 $θ=(X^TX)^{−1}X^Ty$ 。对于给定 m 和n 的值，这个方程中 θ, X, y 的维数分别是多少？

• X ：14×3, y ：14×1, θ ：3×3

• ✅ X ：14×4, y ：14×1, θ ：4×1

• X ：14×3, y ：14×1, θ ：3×1

• X ：14×4, y ：14×4, θ ：4×4

④ 第 4 题

假设您有一个数据集，每个示例有 m = 100,0000 个示例和 n = 20,0000 个特征。你想用多元线性回归来拟合参数 θ 到我们的数据。你更应该用梯度下降还是正规方程？

• ✅ 梯度下降，因为正规方程中$θ=(X^TX)^{−1}$中计算非常慢

• 正规方程，因为它提供了一种直接求解的有效方法

• 梯度下降，因为它总是收敛到最优 θ

• 正规方程，因为梯度下降可能无法找到最优θ

⑤ 第 5 题

以下哪些是使用特征缩放的原因？

• 它可以防止梯度下降陷入局部最优

• 它通过降低梯度下降的每次迭代的计算成本来加速梯度下降

• ✅ 它通过减少迭代次数来获得一个好的解，从而加快了梯度下降的速度

• 它防止矩阵$X^TX$（用于正规方程）不可逆（奇异/退化）

📚 References

• 🤖 吴恩达机器学习经典名课【中英字幕】

• 💠 黄海广 - 斯坦福大学2014机器学习教程中文笔记

• 🍧 90题细品吴恩达《机器学习》，感受被刷题支配的恐惧

• 🥩 吴恩达机器学习 课后实验 python实现

• 🍦 吴恩达机器学习与深度学习作业目录

• 👘《周志华 - 机器学习》