🍜 逻辑回归 Logistic Regression
一、分类问题 Classification
在这个以及接下来的几个视频中,开始介绍分类问题。
在分类问题中,你要预测的变量是离散的值,我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的。

我们从二元的分类问题开始讨论。
我们将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量 y ∈ 0,1 ,其中 0 表示负向类,1 表示正向类。
如下我们用一条直线来拟合这些数据,并设置一个阈值:
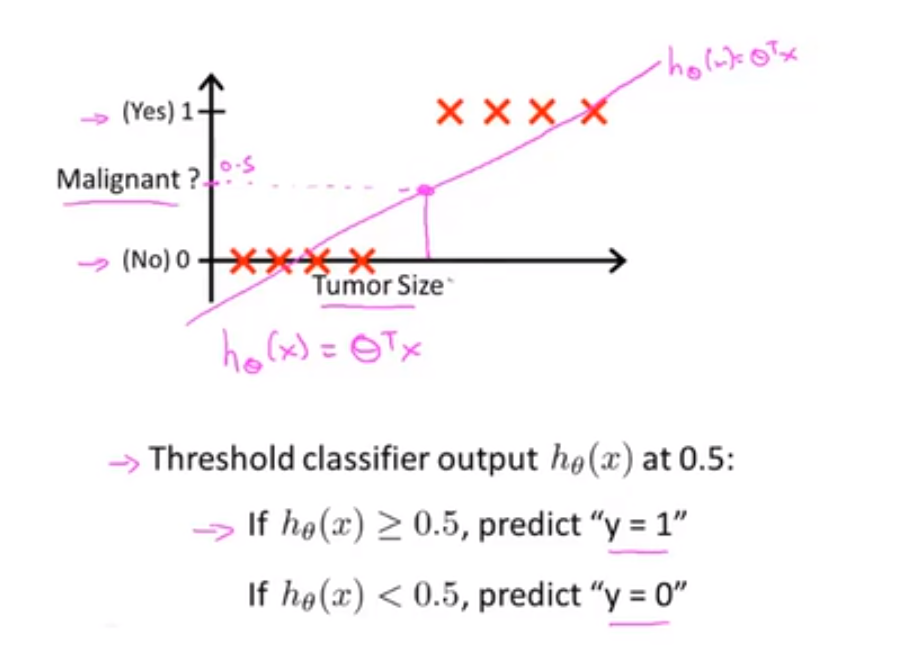
假设我们设置的阈值为 0.5,则如果我们的假设函数的值 大于 0.5,则为正向类(恶性肿瘤),如果假设函数的值 小于 0.5,则为负向类(良性肿瘤)
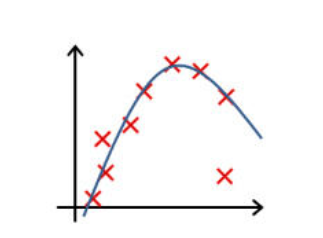
这样看起来线性回归已经很好的解决了这个问题了,但是,如果我们的数据集中存在这样的一点,如下所示:
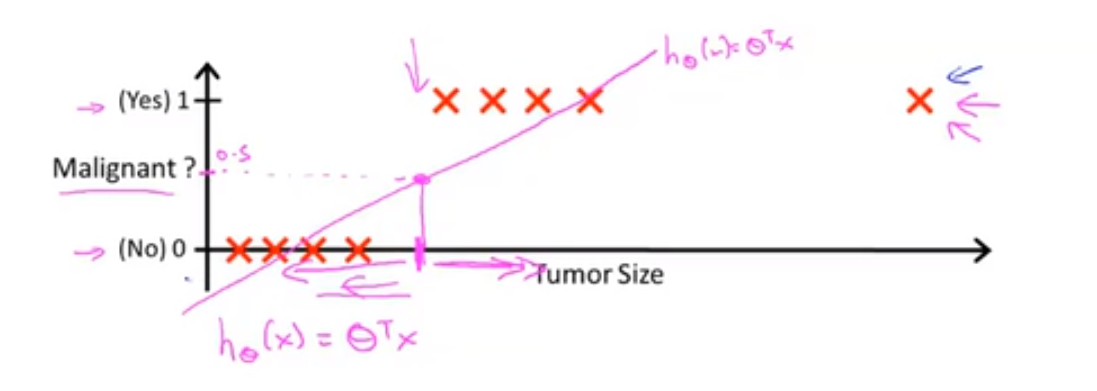
如果仍然采用线性回归,那么我们得到的就是另一条直线,如果我们仍将阈值设置为 0.5,显然会得到一些错误的预测:

对于分类问题, 取值必定为 0 或者 1,但如果我们采用线性回归算法来解决一个分类问题,那么假设函数的输出值可能远大于 1,或者远小于0,即使所有训练样本的标签都等于 0 或 1。所以我们在接下来的要研究的算法就叫做逻辑回归算法,这个算法的性质是:它的输出值永远在 0 到 1 之间。
顺便说一下,🚩 逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签取值离散的情况,如:1 0 0 1。
接下来,我们将开始学习逻辑回归算法的细节。
二、假说表示 Hypothesis Representation
在这段视频中,我要给你展示假设函数的表达式,也就是说,在分类问题中,要用什么样的函数来表示我们的假设。此前我们说过,希望我们的分类器的输出值在 0 和 1 之间,因此,我们希望想出一个满足这个性质的假设函数。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。 逻辑回归模型的假设是 $h_θ(x) = g(θ^TX)$: 其中: X 代表特征向量,g 代表**逻辑函数(logistic function)**或者说 S 形函数(Sigmoid function),公式为:$g(z) = \frac{1}{1+e^{-z}}$ 。
python代码实现:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))该函数的图像为:
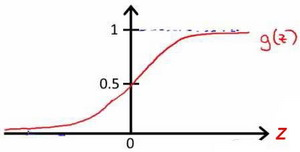
🔴 于是,我们得到假设函数:$h_θ(x) = \frac{1}{1+e^{-θ^TX}}$
⭐ $h_θ(x)$ 的作用是,对于给定的输入变量,根据选择的参数计算输出变量 = 1 的可能性(estimated probablity that y = 1 on input x)即 $h_θ(x) = P(y = 1 | x;θ)$
例如,如果对于给定的 x,通过已经确定的参数计算得出 $h_θ(x) = 0.7$,则表示有70%的几率 y 为正向类,相应的 y 为负向类的几率为 1-0.7=0.3 。
三、决策边界 Decision Boundary
现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。

在逻辑回归中,我们预测:
当 $h_Θ(x) >= 0.5$ 时,预测 $y = 1$ 。
当 $h_Θ(x) < 0.5$ 时,预测 $y = 0$。
根据上面绘制出的 S 形函数图像,我们知道当
$z = 0$ 时:$g(z) = 0.5$
$z > 0$ 时:$g(z) > 0.5$
$z < 0$ 时:$g(z) < 0.5$
又 $z = Θ^Tx$ ,即 :$Θ^Tx >= 0$ 时 ,预测 $y = 1$
$Θ^Tx < 0$ 时 ,预测 $y = $0
💬 现在假设我们有一个模型,并且参数 Θ 是向量 $\begin{bmatrix} -3 \1 \ 1 \end{bmatrix}$ (后续我们将讲解如何拟合参数) 。
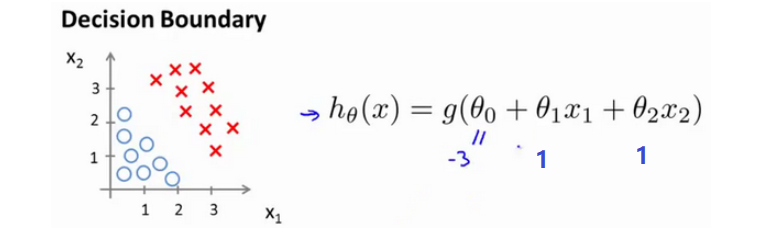
则当 $\begin{bmatrix} -3 & 1 & 1 \end{bmatrix} \begin{bmatrix} x_0 \ x_1 \ x_2\end{bmatrix} ≥ 0$ 即 $-3 + x_1 + x2 ≥ 0$,即 $x_1 + x2 ≥ 3$ 时,模型将预测 y = 1。
🔴 我们可以绘制 $x_1 + x_2 = 3$ 直线,这条线便是我们模型的分界线,将预测为1的区域和预测为 0的区域分隔开。这条直线就称为决策边界 decision boundary
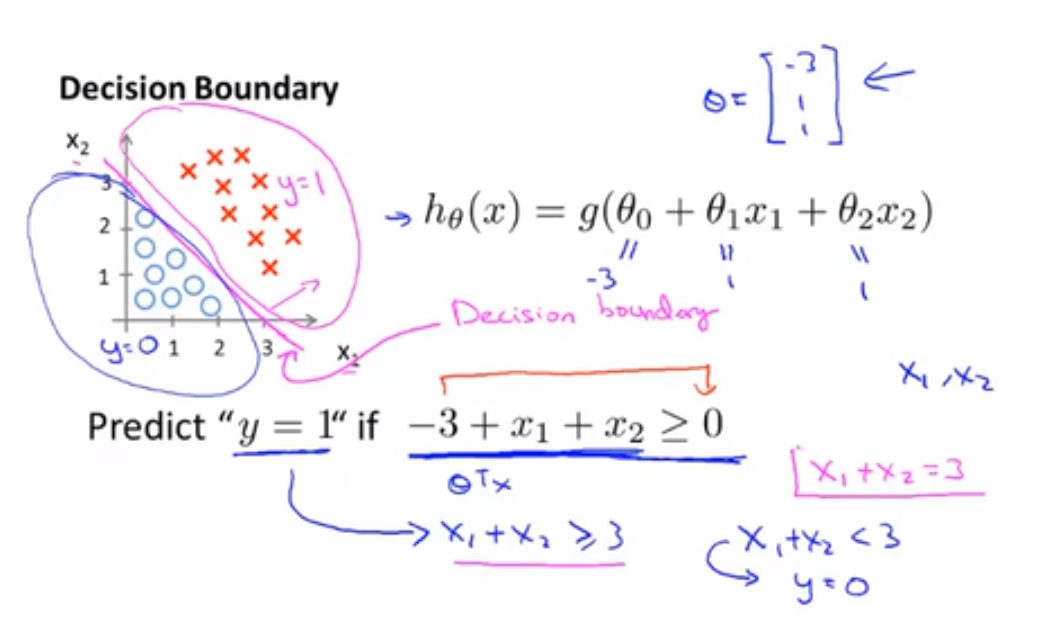
假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?

因为需要用曲线才能分隔 y = 0 的区域和 y = 1 的区域,我们需要二次方特征:θ 取值 $\begin{bmatrix} -1 \ 0 \ 0 \ 1 \ 1 \end{bmatrix}$,则我们得到的判定边界是 $-1 + x_1^2 + x_2^2 ≥ 0$ ,恰好是圆点在原点且半径为 1 的圆形。
🚩 强调:决策边界不是训练集的属性,而是假设本身及其参数的属性,只要给定了参数向量 θ ,那么决定边界就确定了。我们不是用训练集来定义决策边界的,我们用训练集来拟合参数 θ(后续我们将谈论如何拟合)
💡 我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
四、代价函数 Cost Function
在这段视频中,我们要介绍如何拟合逻辑回归模型的参数 θ 。具体来说,我要定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。

对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于,当我们将 $h_θ(x) = \frac{1}{1+e^{-θ^TX}}$ 带入到这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数(non-convexfunction),即有很多个局部最小值,这将影响梯度下降算法寻找全局最小值。

线性回归的代价函数为:$J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)}) - y^{(i)})^2$,我们重新定义逻辑回归的代价函数为:🔴 $J(θ_0,θ_1) = \frac{1}{m}\sum_{i=1}^{m}Cost(h_θ(x^{(i)}),y^{(i)})$,其中
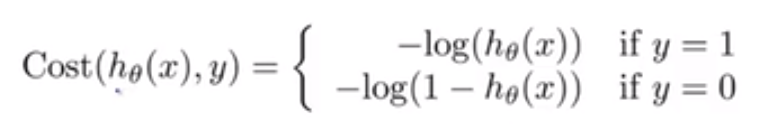
假设函数 $h_θ(x)$ 与 代价函数 $Cost(h_θ(x),y)$ 之间的关系如下图所示:
y = 1
可以看见,当代价函数 = 0 时,即假设函数最佳拟合,此时我们预测结果(假设函数)为 1 正向类。形象的说,如果我们预测的结果为 1,那么我们付出的代价为 0
如果我们预测值为 0,可以看见,此时的代价函数趋向于无穷,也即,这是个错误的预测,如果我们非要做出这样的预测,那将付出很大的代价
y = 0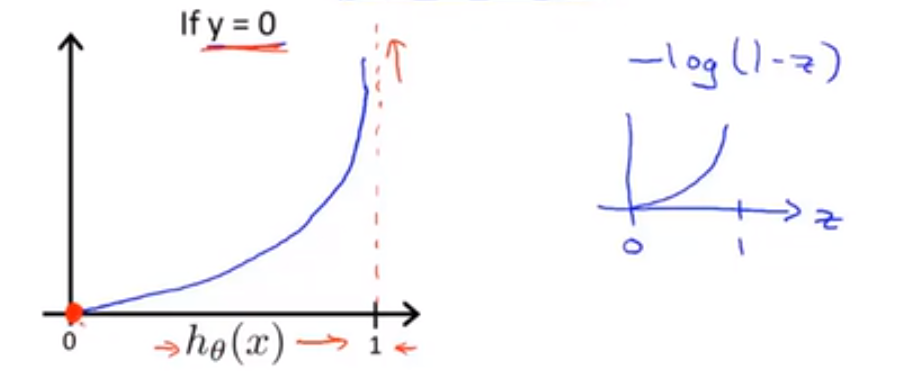
可以看见,当代价函数 = 0 时,即假设函数最佳拟合,此时我们预测结果(假设函数)为 0 正向类。形象的说,如果我们预测的结果为 0,那么我们付出的代价为 0
如果我们预测值为 1,可以看见,此时的代价函数趋向于无穷,也即,这是个错误的预测,如果我们非要做出这样的预测,那将付出很大的代价
五、简化的代价函数和梯度下降 Simplified Cost Function and Gradient Descent
在本节中,我们将会找出一种稍微简单一点的方法来写代价函数,来替换我们现在用的方法。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。因此,学完本节,你就应该知道如何实现一个完整的 logistic 回归算法。
这是逻辑回归的代价函数:

我们可以对这个式子进行合并,使得两段函数变成一个函数,有利于我们进行梯度下降:
⭐逻辑回归的代价函数: 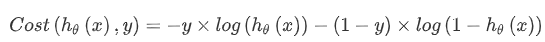
Python 代码实现:
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))根据代价函数,为了拟合出参数,该怎么做呢?我们要找到让代价函数 J 取得全局最小值的参数 θ,这时假设函数最大程度拟合数据集。
最小化代价函数的方法,是使用梯度下降法(gradient descent)。这是逻辑回归的代价函数:
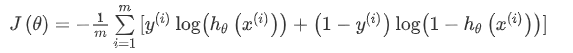
⭐ 这是我们通常用的梯度下降法的模板:

我们要反复更新每个参数,用这个式子来更新,就是用它自己减去学习率 α 乘以后面的微分项。⭐求导后得到:
所以,如果你有 n 个特征,也就是说: $\begin{bmatrix} θ_0 \ θ_1 \ θ_2 \ ... \ θ_n\end{bmatrix}$ ,参数向量包括 $θ_0,θ_1$ 一直到 $θ_n$,那么你就需要用上面这个式子来同时更新所有的值。
现在,如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地发现,这个式子正是我们用来做线性回归梯度下降的。
🚩 那么,线性回归和逻辑回归是同一个算法吗?实际上,假设的定义发生了变化。
对于线性回归假设函数:$h_θ(x) = θ_0x_0 + θ_1x_1 + θ_2x_2 + ... + + θ_nx_n $
而现在逻辑函数假设函数:$h_θ(x) = \frac{1}{1+e^{-θ^TX}}$
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
最后还有一点,我们之前在谈线性回归时讲到的特征缩放,我们看到了特征缩放是如何提高梯度下降的收敛速度的,这个特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。
六、高级优化 Advanced Optimization
在上一节中,我们讨论了用梯度下降的方法最小化逻辑回归中代价函数 J(θ)。在本节中,我们将学习一些高级优化算法和一些高级的优化概念,利用这些方法,我们就能够使通过梯度下降使得进行逻辑回归的速度大大提高,而这也将使算法更加适合解决大型的机器学习问题,比如,我们有数目庞大的特征量。
现在我们换个角度来看什么是梯度下降,我们有个代价函数 J(θ),而我们想要使其最小化,那么我们需要做的是编写代码,当输入参数 θ 时,它们会计算出两样东西: J(θ) 以及 J(θ) 等于 0、1 直到 n 时的偏导数项。

假设我们已经完成了可以实现这两件事的代码,那么梯度下降所做的就是反复执行这些更新。
然而梯度下降并不是我们可以使用的唯一算法,还有其他一些算法,更高级、更复杂。如果我们能用这些方法来计算代价函数和偏导数项两个项的话,那么这些算法就是为我们优化代价函数的不同方法,共轭梯度法 BFGS (变尺度法) 和L-BFGS (限制变尺度法) 就是其中一些更高级的优化算法,它们需要有一种方法来计算 ,以及需要一种方法计算导数项,然后使用比梯度下降更复杂的算法来最小化代价函数。这三种算法的具体细节超出了本门课程的范畴。

这三种算法有许多优点:
一个是使用这其中任何一个算法,你通常不需要手动选择学习率 ,所以对于这些算法的一种思路是,给出计算导数项和代价函数的方法,你可以认为算法有一个智能的内部循环,而且,事实上,他们确实有一个智能的内部循环,称为线性搜索(line search)算法,它可以自动尝试不同的学习速率 ,并自动选择一个好的学习速率 ,因此它甚至可以为每次迭代选择不同的学习速率,那么你就不需要自己选择。这些算法实际上在做更复杂的事情,不仅仅是选择一个好的学习速率,所以它们往往最终比梯度下降收敛得快多了,不过关于它们到底做什么的详细讨论,已经超过了本门课程的范围。
七、多类别分类:一对多 Multiclass Classification_ One-vs-all
在本节中,我们将谈到如何使用逻辑回归 (logistic regression)来解决多类别分类问题,具体来说,我们将学习 "一对多" (one-vs-all) 的分类算法。
先看这样一些例子。
第一个例子:假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里,或者说可以自动地加上标签,那么,你也许需要一些不同的文件夹,或者不同的标签来完成这件事,来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好的邮件,那么,我们就有了这样一个分类问题:其类别有四个,分别用 y = 1、y = 2、y = 3、 y = 4 来代表。
第二个例子是有关药物诊断的:如果一个病人因为鼻塞来到你的诊所,他可能并没有生病,用 y = 1 这个类别来代表;或者患了,用 y = 2 来代表;或者得了流感用 y = 3 来代表。
第三个例子:如果你正在做有关天气的机器学习分类问题,那么你可能想要区分哪些天是晴天、多云、雨天、或者下雪天,对上述所有的例子, y 可以取一个很小的数值,一个相对"谨慎"的数值,比如1 到3、1 到 4 或者其它数值,以上说的都是多类分类问题。
顺便一提的是,对于下标是0 1 2 3,还是 1 2 3 4 都不重要,我更喜欢将分类从 1 开始标而不是 0,其实怎样标注都不会影响最后的结果。

对于之前的一个二元分类问题,我们的数据看起来可能是像这样:
对于一个多类分类问题,我们的数据集或许看起来像这样:
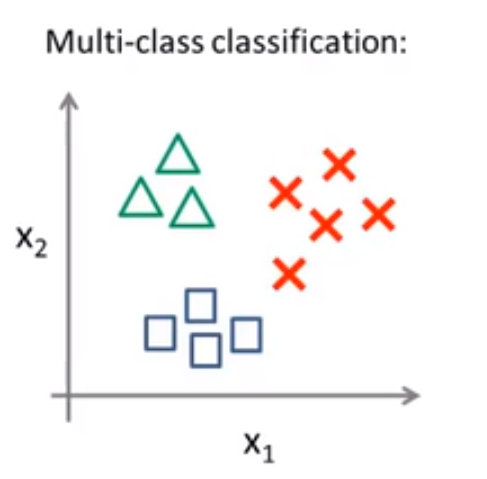
我用 3 种不同的符号来代表3个类别,❓ 问题就是给出 3 个类型的数据集,我们如何得到一个学习算法来进行分类呢?
现在我们有一个训练集,好比上图表示的有3个类别,我们用三角形表示 y = 1 ,方框表示 y = 2,叉叉表示 y = 3。我们下面要做的就是使用一个训练集,⭐ 将其分成 3 个二元分类问题。
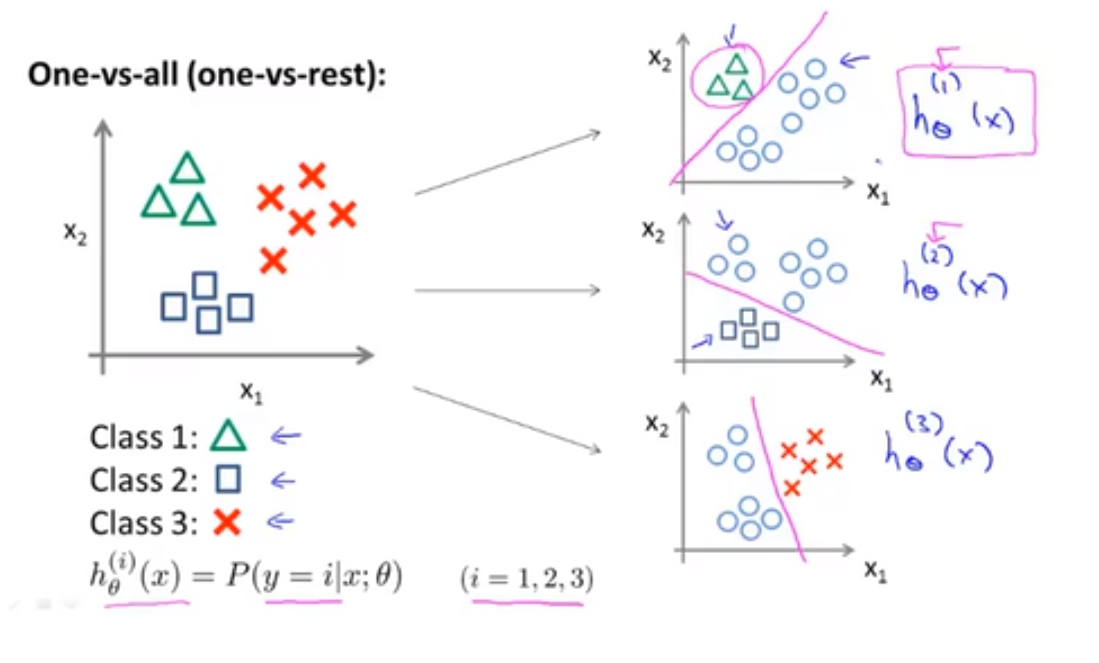
比如:这里的三角形是正样本,而圆形代表负样本。可以这样想,设置三角形的值为 1,圆形的值为 0,下面我们来训练一个标准的逻辑回归分类器,这样我们就得到一个正边界。
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(y = 1),然后将其他所有类都标记为负向类,这个模型记作 $h_θ^{(1)}(x)$。接着,类似地第我们选择另一个类标记为正向类(y = 2),再将其它类都标记为负向类,将这个模型记作 $h_θ^{(2)}(x)$ ,依此类推。 最后我们得到一系列的模型简记为: 其中 $h_θ^{(i)}(x) = P(y = i | x,θ)$ ,其中:i = (1,2,3...k)
🚩 最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量,即 $max h_θ^{(i)}(x)$。
⭐ 小结
总结一下逻辑回归算法:
**假设函数 **:预测一条直线分割数据集 - $h_θ(x) = \frac{1}{1+e^{-θ^TX}}$
代价函数:当代价函数取得最小值时(取决于 θ),假设函数将最佳拟合数据集 -
(批量)梯度下降:使用梯度下降算法来求出代价函数 $J(θ_0,θ_1)$ 的最小值 -

多类别逻辑回归:将其分为若干个二元分类问题,将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量
✍ Quiz — Week 3 | 1 逻辑回归
① 第 1 题
假设您已经训练了一个逻辑分类器,它在一个新示例 x 上输出一个预测 hθ(x)=0.4。这意味着(选出所有正确项):
我们对 P(y=0∣x;θ) 的估计是 0.4
我们对 P(y=1∣x;θ) 的估计是 0.6
✅ 我们对 P(y=0∣x;θ) 的估计是 0.6
✅ 我们对 P(y=1∣x;θ) 的估计是 0.4
② 第 2 题
假设您有以下训练集,并拟合 logistic 回归分类器 $h_θ(x)=g(θ_0+θ_1x_1+θ_2x_2)$
x1 |
x2 |
y |
|---|---|---|
1 |
0.5 |
0 |
1 |
1.5 |
0 |
2 |
1 |
1 |
3 |
1 |
0 |
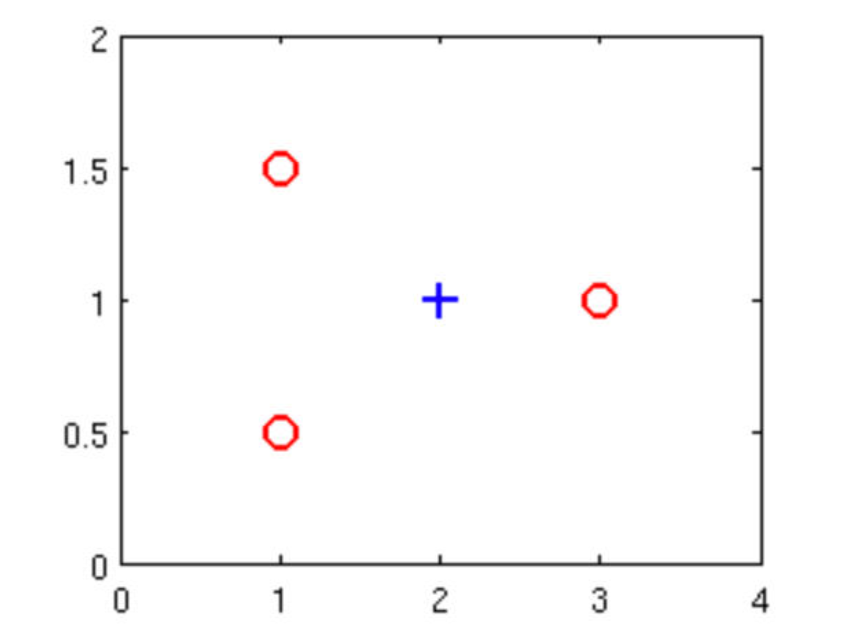
以下哪项是正确的?选出所有正确项
✅ 添加多项式特征(例如,使用 $h_θ(x)=g(θ_0+θ_1x_1+θ_2x_2+θ_3x_{12}+θ_4x_1x_2+θ_5x_{22})$ )可以增加我们拟合训练数据的程度
✅ 在θ的最佳值(例如,由 fminunc 找到)处,J(θ) ≥ 0
添加多项式特征(例如,使用 $h_θ(x)=g(θ_0+θ_1x_1+θ_2x_2+θ_3x_{12}+θ_4x_1x_2+θ_5x_{22})$ )将增加 J(θ),因为我们现在正在对更多项进行求和
如果我们训练梯度下降迭代足够多次,对于训练集中的一些例子 $x^{(i)}$,可能得到 $h_θ(x^{(i)}) > 1$
③ 第 3 题
对于逻辑回归,梯度由 $\frac{\partial}{\partial \theta_j}J(\theta)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j$ 出。以下哪项是学习率为 α 的逻辑回归的正确梯度下降更新?选出所有正确项
$\theta := \theta - \alpha \frac{1}{m} \sum_{i=1}^m{ \left(\theta^T x - y^{(i)}\right) x^{(i)}}$
✅ $\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m{ \left(\frac{1}{1 + e^{-\theta^T x^{(i)}}} - y^{(i)}\right) x_j^{(i)}}$(同时更新所有 j)
$\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m{ (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}}$(同时更新所有 j)
✅ $\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^m{ (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}}$(同时更新所有 j)
④ 第 4 题
以下哪项陈述是正确的?选出所有正确项
❌ 对于逻辑回归,梯度下降有时会收敛到一个局部最小值(并且无法找到全局最小值)。这就是为什么我们更喜欢更先进的优化算法,如 fminunc(共轭梯度/BFGS/L-BFGS/等等)
更先进的优化算法在于它们的效率更高,但任然无法避免困在局部最小值的问题
✅ sigmoid 函数 $g(z) = \frac{1}{1 + e^{-z}}$ 数值永远不会大于1
✅ 用 m ≥ 1 个例子训练的逻辑回归的代价函数J(θ)总是大于或等于零
使用线性回归+阈值的方法做分类预测,总是很有效的
⑤ 第 5 题
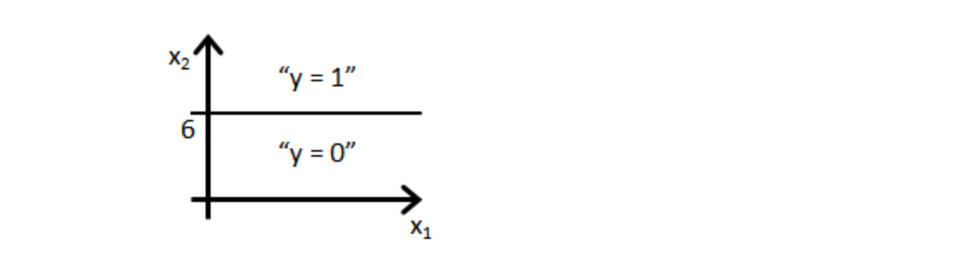
假设训练一个逻辑回归分类器 $h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$ 。假设 θ0=6, θ1=−1, θ2=0,下列哪个图表示分类器找到的决策边界?
✅ 图 1:
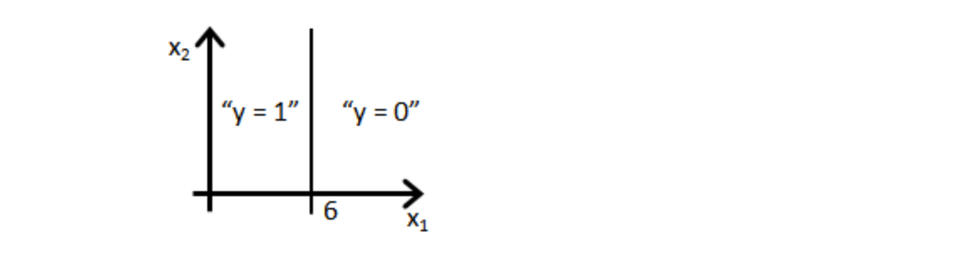
图 2:
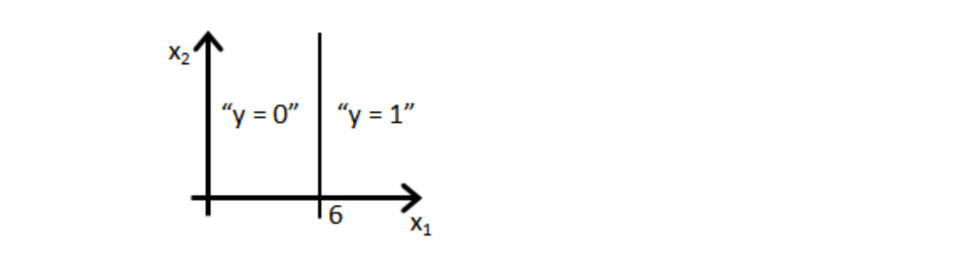
图 3:
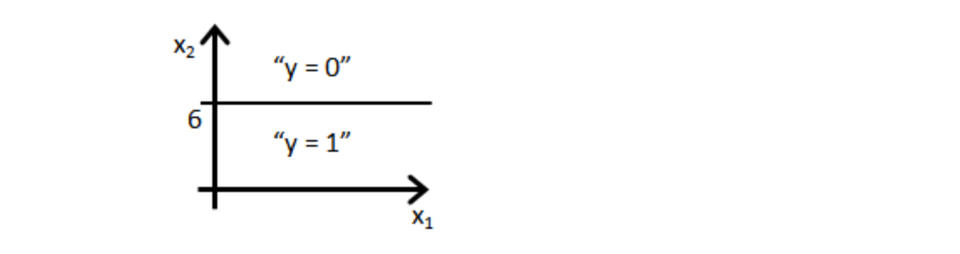
图 4:
🥧 正则化 Regularization
一、过拟合的问题 The Problem of Overfitting
到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合(over-fitting)的问题,可能会导致它们效果很差。
在本节中,我们将了解什么是过度拟合问题,并且在此之后接下来的几个视频中,我们将谈论一种称为正则化(regularization)的技术,它可以改善或者减少过拟合问题。
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是无法推广到新的数据。
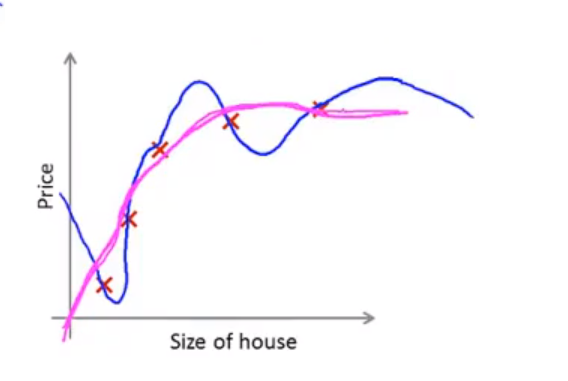
💬 下图是一个回归问题的例子:
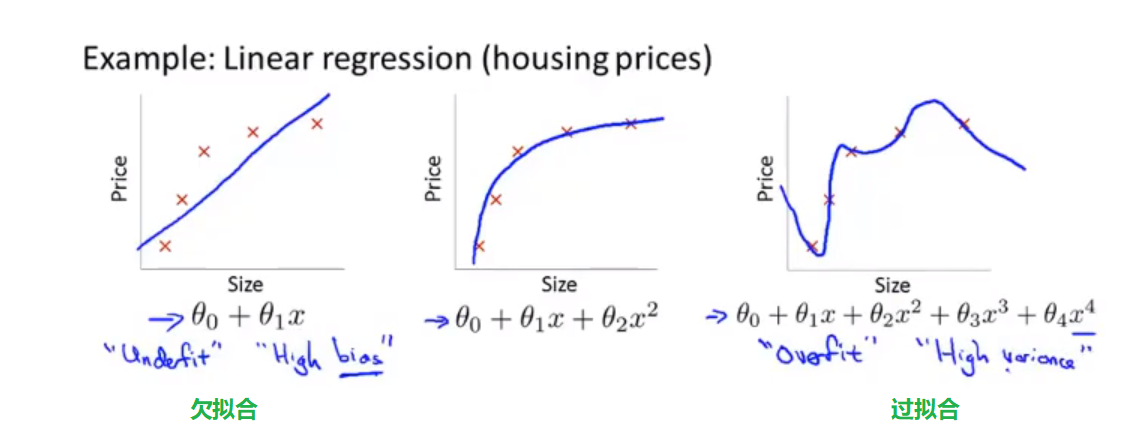
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;
第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好;

而中间的模型似乎最合适。
💬 分类问题中也存在这样的问题:
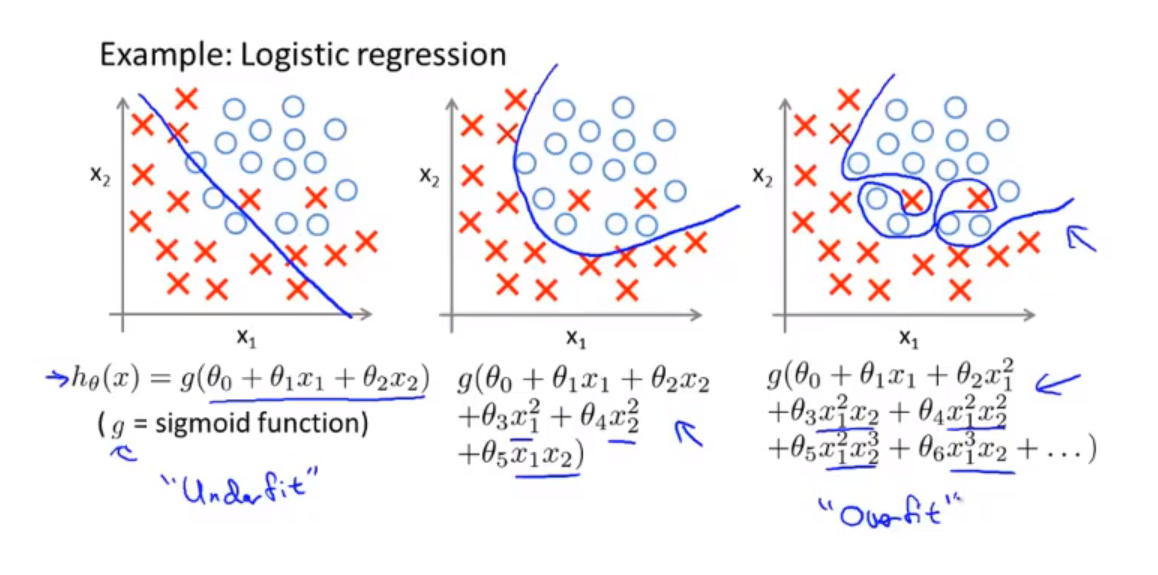
🚩 就以多项式理解, x 的次数越高,拟合的越好,但相应的预测的能力就可能变差。
⚒ 如果我们发现了过拟合问题,应该如何处理?
只保留重要特征,丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
⭐ 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
二、代价函数 Cost Function
上面的回归问题中如果我们的模型是:$h_θ(x) = θ_0 + θ_1x_1 + θ_2x_2^2 + θ_3x_3^3 + θ_4x_4^4$ 我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于 0 的话,我们就能很好的拟合了。 所以我们要做的就是在一定程度上减小这些参数 的值,这就是正则化的基本方法。
我们决定要减少 θ3 和 θ4 的大小,我们要做的便是修改代价函数,在其中θ3 和 θ4 设置一点惩罚。这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的 θ3 和 θ4。 比如修改后的代价函数如下:
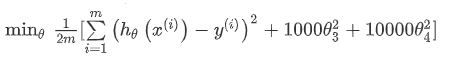
此处的 1000 和 10000 只是随便设置的一个较大的值,通过这样的代价函数,使得我们获得的 θ3 和 θ4 趋向于 0
通过这样的代价函数选择出的 θ3 和 θ4 对预测结果的影响就比之前要小许多。假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:
⭐ 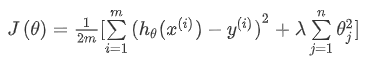
其中 λ 又称为正则化参数(Regularization Parameter)。 注:根据惯例,我们不对 λ 进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示:
🚩 如果选择的正则化参数 λ 过大,则会把所有的参数都最小化了,导致模型变成 $h_θ(x) = θ_0 $,也就是下图所示的情况,造成欠拟合。

那为什么增加的一项 $ λ = \sum_{j=1}^n θ_j^2$ 可以使的值减小呢? 因为如果我们令 λ 的值很大的话,为了使Cost Function 尽可能的小,所有的 θ 的值(不包括 θ0 )都会在一定程度上减小。 但若 λ 的值太大了,那么 θ (不包括 θ0)都会趋近于0,这样我们所得到的只能是一条平行于 x 轴的直线。 所以对于正则化,我们要取一个合理的 λ 的值,这样才能更好的应用正则化。
三、线性回归的正则化 Regularized Linear Regression
基于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。其中梯度下降算法:
正则化线性回归的代价函数为:
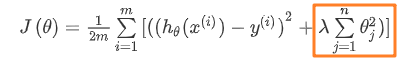
如果我们要使用梯度下降法令这个代价函数最小化,因为我们未对 θ0 进行正则化,所以梯度下降算法将分两种情形:
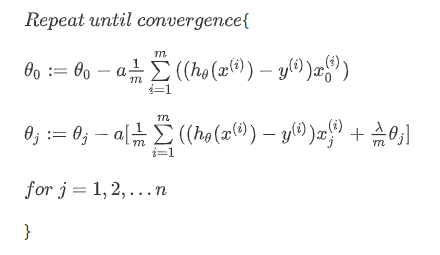
对上面的算法中 j = 1,2,3...n 时的更新式子进行调整可得:
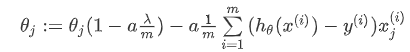
可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令 θ 值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型,方法如下所示:
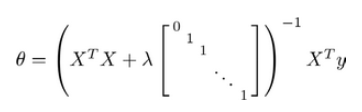
图中的矩阵尺寸为 (n+1) * (n+1)
四、逻辑回归模型的正则化
针对逻辑回归问题,我们在之前的课程已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数,接下来学习了更高级的优化算法,这些高级优化算法需要你自己设计代价函数。
这是逻辑回归的代价函数:
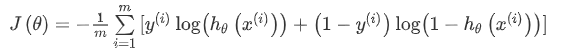
⭐ 我们也给逻辑回归的代价函数增加一个正则化的表达式,得到代价函数:
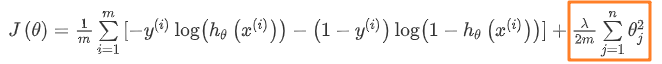
Python代码:
import numpy as np
def costReg(theta, X, y, learningRate):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X*theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))
reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:theta.shape[1]],2))
return np.sum(first - second) / (len(X)) + reg要最小化该代价函数,通过求导,得出梯度下降算法为(因为我们未对 θ0 进行正则化,所以梯度下降算法将分两种情形):
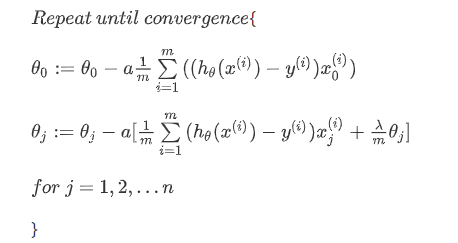
对上面的算法中 j = 1,2,3...n 时的更新式子进行调整可得:
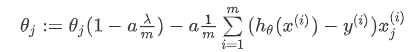
🚨 注意:
虽然正则化的逻辑回归中的梯度下降和正则化的线性回归中的表达式看起来一样,但由于两者的 $h_θ(x)$ 不同所以还是有很大差别。
θ0 不参与其中的任何一个正则化。
⭐ 小结
总结一下正则化的相关知识:
过拟合 / 欠拟合:
欠拟合:不能很好地适应训练集
过拟合:过于强调拟合训练集,使得预测数据的能力变差
正则化:解决过拟合问题的两个方法:
只保留重要特征:丢弃一些不能帮助我们正确预测的特征。
正则化:保留所有的特征,但是减少参数的大小(magnitude)。
线性回归的正则化:
假设函数不变
代价函数:
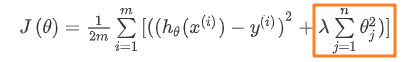
梯度下降:
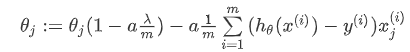
逻辑回归的正则化:
假设函数不变
代价函数:
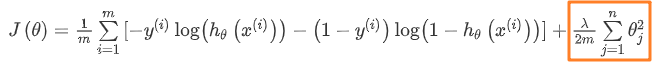
梯度下降:
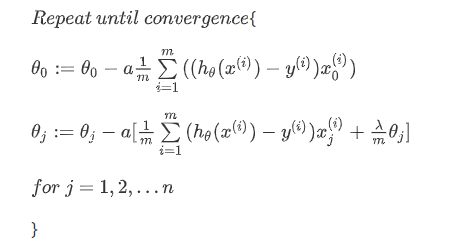
✍ Quiz — Week 3 | 2 正则化
① 第 1 题
你正在训练一个分类逻辑回归模型。以下哪项陈述是正确的?选出所有正确项
将正则化引入到模型中,总是能在训练集上获得相同或更好的性能
在模型中添加许多新特性有助于防止训练集过度拟合
将正则化引入到模型中,对于训练集中没有的例子,总是可以获得相同或更好的性能
✅ 向模型中添加新特征总是会在训练集上获得相同或更好的性能
② 第 2 题
假设您进行了两次逻辑回归,一次是 λ=0 ,一次是 λ=1。其中一次,得到参数 $\theta = \begin{bmatrix} 81.47 \ 12.69 \end{bmatrix}$,另一次,得到 $\theta = \begin{bmatrix} 13.01 \ 0.91 \end{bmatrix}$。 但是,您忘记了哪个 λ 值对应于哪个 θ 值。你认为哪个对应于 λ=1?
$\theta = \begin{bmatrix} 81.47 \ 12.69 \end{bmatrix}$
✅ $\theta = \begin{bmatrix} 13.01 \ 0.91 \end{bmatrix}$
③ 第 3 题
以下关于正则化的陈述哪一个是正确的?选出所有正确项
使用太大的 λ 值可能会导致您的假设与数据过拟合;这可以通过减小 λ 来避免
使用非常大的值 λ 不会影响假设的性能;我们不将 λ 设置为太大的唯一原因是避免数值问题
✅ 考虑一个分类问题。添加正则化可能会导致分类器错误地分类某些训练示例(当不使用正则化时,即当 λ = 0 时,它正确地分类了这些示例)
由于逻辑回归的输出值 0≤hθ(x)≤1,其输出值的范围无论如何只能通过正则化来“缩小”一点,因此正则化通常对其没有帮助
④ 第 4 题
下列哪一个图片的假设与训练集过拟合?
✅ 图 1:
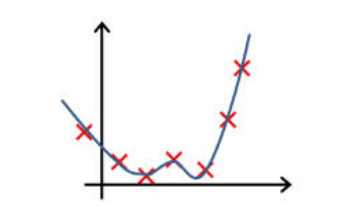
图 2:
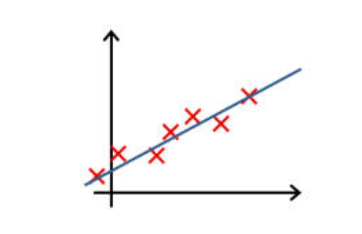
图 3:
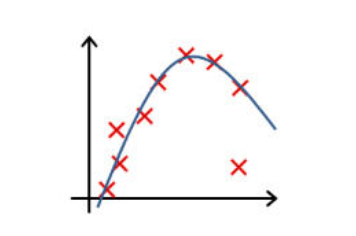
图 4:
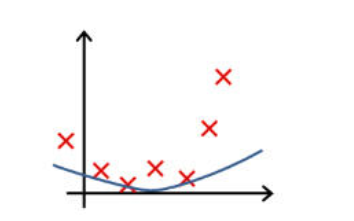
⑤ 第 5 题
下列哪一个图片的假设与训练集欠拟合?
✅ 图 1:
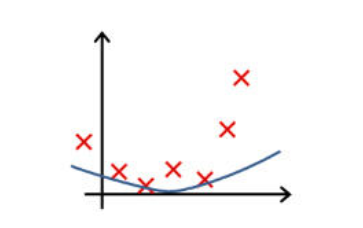
图 2:

图 3:
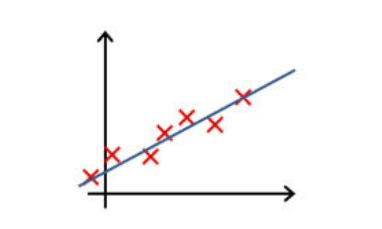
图 4: