将数字从小到大的顺序排列
冒泡排序
冒泡排序重复"从序列右边开始比较相邻两个数字的大小,再根据结果交换两个数字的位置"。数字像泡泡一样,慢慢从右往左"浮"到序列的顶端。
在序列的最右边放置一个天平,比较天平两边的数字。如果右边的数字较小,则交换位置。完成后,往左移一个位置比较两个数字大小,重复操作直到天平到达序列的最左边为止。一轮操作后,序列中最小的数字就会移动到最左边。第二轮时候移动到左边第二个位置为止,重复此操作,直到最终排序完成。

总结假设序列中有n个数,第1轮需要比较n-1次,第2轮需要比较n-2次。因此,总的次数为总的比较次数为(n-1)+(n-2)+…+1≈n2/2。这个比较次数恒定为该数值,和输入数据的排列顺序无关。
不过,交换数字的次数和输入数据的排列顺序有关。假设出现某种极端情况,如输入数据正好以从小到大的顺序排列,那么便不需要任何交换操作;反过来,输入数据要是以从大到小的顺序排列,那么每次比较数字后便都要进行交换。因此,冒泡排序的时间复杂度为O(n2/2)。
选择排序
选择排序重复"从待排序的序列中寻找最小值,将其与待排序序列中最左边的数字进行交换",在序列中寻找最小值时使用的是线性查找。

将数字1~9排序线性查找在数据中找到最小值1将其与6位置进行交换,最小值1归位。(如果最小值已经在最左端,就不需要任何操作)。在余下的数据中继续寻找最小值,于是找到了2,将其与6交换位置,最小值2归位。重复操作直到最终排序完成。

总结选择排序使用了线性查找来寻找最小值,因此在第1轮中需要比较n-1个数字,第2轮需要比较n-2个数字……到第n-1轮的时候就只需比较1个数字了。因此,总的比较次数与冒泡排序的相同,都是(n-1)+(n-2)+…+1≈O(n2/2)次。每轮中交换数字的次数最多为1次。如果输入数据就是按从小到大的顺序排列的,便不需要进行任何交换。选择排序的时间复杂度也和冒泡排序的一样,都为O(n2)。
插入排序
插入排序是一种从序列左端开始依次对数据进行排序的算法,排序过程中左侧的数据陆续归位,右侧留下的就是还未被排序的数据。思路是从右侧未排序区域内取出一个数据,将它插入到已排序区域内合适的位置上。
将数字1~9排序接下来从待排数字中取出最左边的数字3,将它与左边已归位的数字进行比较。若左边数字更大,就交换这两个数字。因为5>3,所以交换位置,至此第2轮操作结束。第3轮取出待排序区域中最左边的数字4,将它与左边的数字5比较,由于5>4,所以交换位置。交换后再把4和左边的3进行比较,发现3<4至此操作结束。重复此操作直至排序完成。
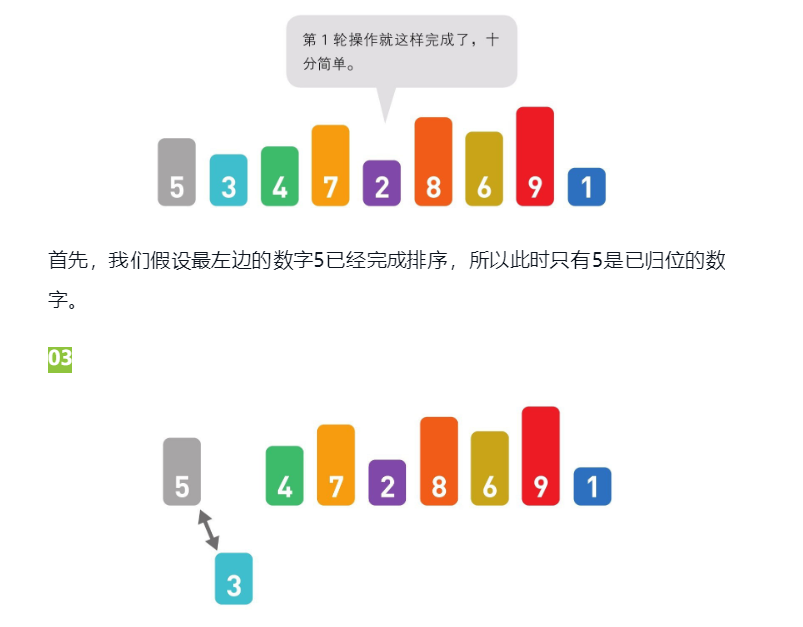
时间复杂度如果取出的数字比左边已归位的数字都要小,就必须不停地比较大小,交换数字,直到它到达序列的最左边为止。在最糟糕的情况下,第2轮需要操作1次,第3轮操作2次……第n轮操作n-1次,所以时间复杂度为O(n2)。
堆排序
堆排序首先在堆中存储所有的数据,并按降序来构建堆。为了排序,需要再从堆中把数据一个个取出来。
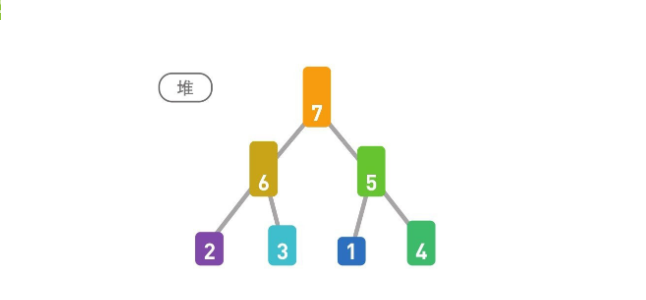
首先取出根结点数字7后,放到数组重新构造堆。重复此操作即可。
归并排序
归并排序会把序列分成长度相同的的两个子序列,当无法继续分时(也就是每个子序列中只有一个数据时),就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
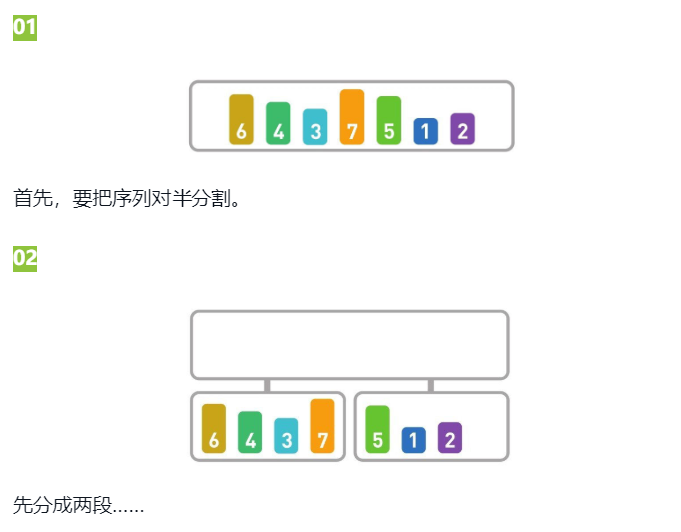
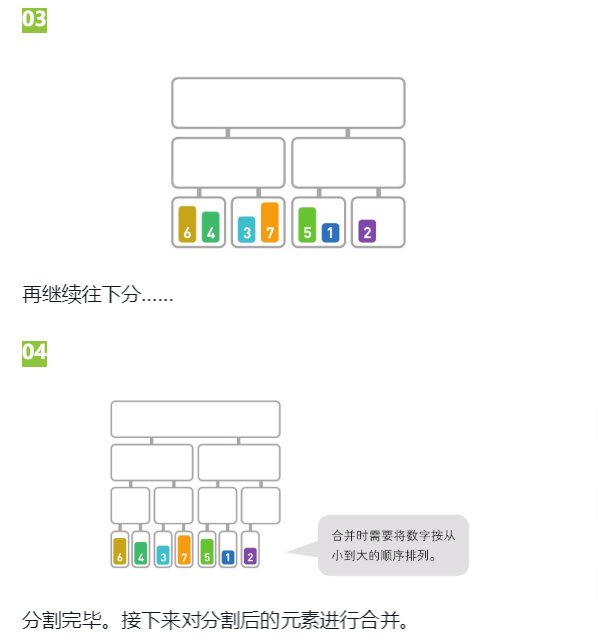
把6和4合并,合并后的顺序为[4,6],接下来把3和7合并,合并后的顺序为[3,7]。接下来我们看看如何合并[4,6]和[3,7]。合并这种含有多个数字的子序列时,要先比较首位数字,在移动较小数字。因为4>3,所以移动3。同样地,再比较序列中剩下的首位数字,因为4<7,所以移动4。
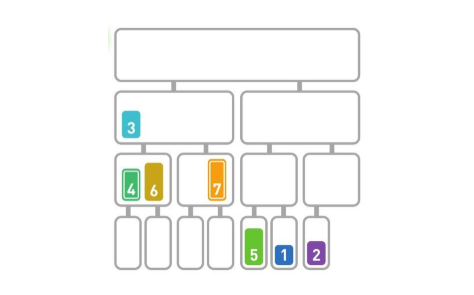
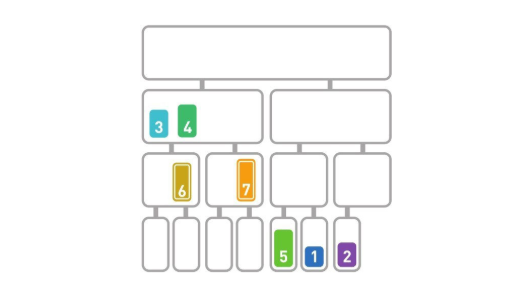
由于6<7,所以移动6,最后移动剩下的7。递归执行上面操作,直到所有的数字都合为一个整体。
时间复杂度无论哪一行都是n个数据,所以每行的运行时间都为O(n)。而将长度为n的序列对半分割直到只有一个数据为止时,可以分成log2n行,因此,总共有log2n行。也就是说,总的运行时间为O(nlogn)。
快速排序
快速排序在序列中随机选择一个基准值,然后将除了基准值以外的数分为"比基准值小的数"和"比基准值大的数"这两个类别。如下👇
[比基准值小的数] 基准值 [比基准值大的数]
接着,对两个"[]"中的数据进行排序之后,整体的排序便完成了,对"[]"里面的数据进行排序同样也会使用快速排序。
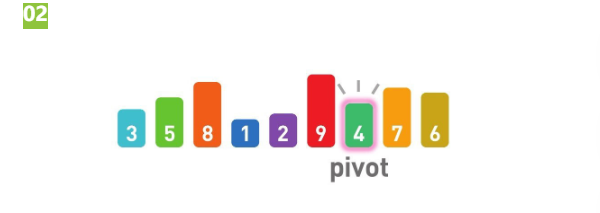
随机选择基准值,为4。首先,比较3和基准值4,因为3<4,所以将3往左移动。接下来比较5和基准值4,因为5>4,所以将5往右移。以此类推得到下面的排序👇。
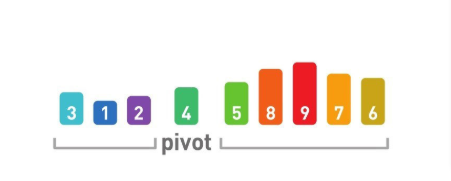
分别对左边和右边的数据进行排序后,就能得到整体的排序。
「时间复杂度为O(logn)」
