🥑 机器学习策略(上)
一、什么是 ML 策略
如何构建你的机器学习项目也就是说机器学习的策略。通过本节我们将能够学到如何更快速高效地优化你的机器学习系统。那么,什么是机器学习策略呢?

我们从一个启发性的例子开始讲,假设你正在调试你的猫分类器,经过一段时间的调整,你的系统达到了90%准确率,但对你的应用程序来说还不够好。
你可能有很多想法去改善你的系统,比如,你可能想我们去收集更多的训练数据吧。或者你会说,可能你的训练集的多样性还不够,你应该收集更多不同姿势的猫咪图片,或者更多样化的反例集。或者你想再用梯度下降训练算法,训练久一点。或者你想尝试用一个完全不同的优化算法,比如Adam优化算法。或者尝试使用规模更大或者更小的神经网络。或者你想试试dropout或者正则化。或者你想修改网络的架构,比如修改激活函数,改变隐藏单元的数目之类的方法。
可选择的方法很多,也很复杂、繁琐。盲目选择、尝试不仅耗费时间而且可能收效甚微。因此,使用快速、有效的策略来优化机器学习模型是非常必要的。
二、正交化 Orthogonalization
机器学习中有许多参数、超参数需要调试。通过每次只调试一个参数,保持其它参数不变,而得到的模型某一性能改变是一种最常用的调参策略,我们称之为正交化方法(Orthogonalization)。
Orthogonalization 的核心在于每次调试一个参数只会影响模型的某一个性能。
对应到机器学习监督式学习模型中,可以大致分成四个独立的“功能”:
Fit training set well on cost function
Fit dev set well on cost function
Fit test set well on cost function
Performs well in real world
其中,第一条优化训练集可以通过使用更复杂NN,使用Adam等优化算法来实现;第二条优化验证集可以通过采用更多训练样本来实现;第三条优化测试集可以通过使用更多的验证集样本来实现;第四条提升实际应用模型可以通过更换验证集,使用新的 cost function 来实现。概括来说,每一种“功能”对应不同的调节方法。而这些调节方法只会对应一个“功能”,相互之间是正交的。
顺便提一下,early stopping 在模型功能调试中并不推荐使用。因为 early stopping 在提升验证集性能的同时降低了训练集的性能。也就是说 early stopping 同时影响两个“功能”,不具有独立性、正交性。
三、单一数字评估指标 Single number evaluation metric
构建、优化机器学习模型时,单值评价指标非常必要。有了量化的单值评价指标后,我们就能根据这一指标比较不同超参数对应的模型的优劣,从而选择最优的那个模型。
举个例子,比如有 A 和 B 两个模型,它们的准确率(Precision)和召回率(Recall)分别如下:
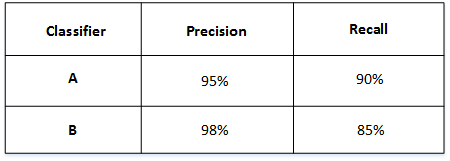
如果只看Precision的话,B模型更好。如果只看Recall的话,A模型更好。实际应用中,我们通常使用单值评价指标F1 Score 来评价模型的好坏。F1 Score综合了Precision和Recall的大小,计算方法如下: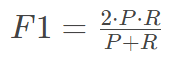
然后得到了A和B模型各自的F1 Score:
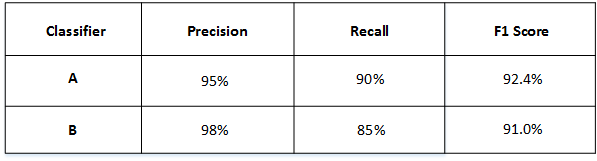
从F1 Score来看,A模型比B模型更好一些。通过引入单值评价指标F1 Score,很方便对不同模型进行比较。
除了F1 Score之外,我们还可以使用平均值作为单值评价指标来对模型进行评估。如下图所示,A, B, C, D, E, F六个模型对不同国家样本的错误率不同,可以计算其平均性能,然后选择平均错误率最小的那个模型(C模型)。
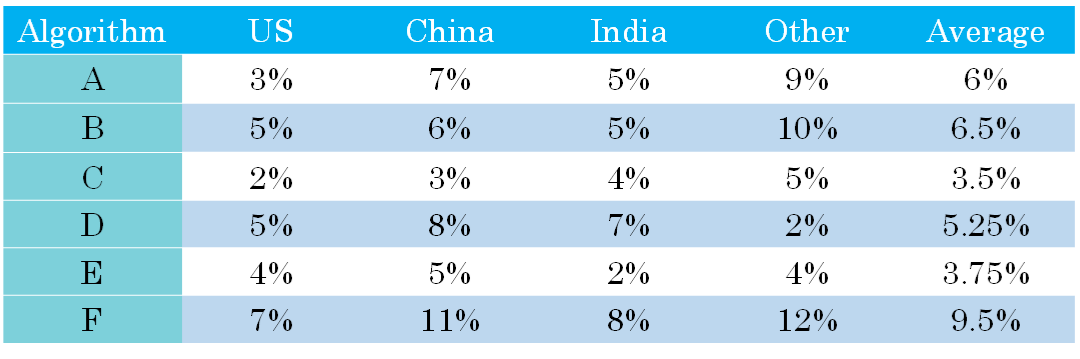
四、满意指标和优化指标 Satisficing and Optimizing metric
有时候,要把所有的性能指标都综合在一起,构成单值评价指标是比较困难的。解决办法是,我们可以把某些性能作为优化指标(Optimizing metic),寻求最优化值;而某些性能作为满意指标(Satisficing metic),只要满足阈值就行了。
举个猫类识别的例子,有A,B,C三个模型,各个模型的Accuracy和Running time如下表中所示:
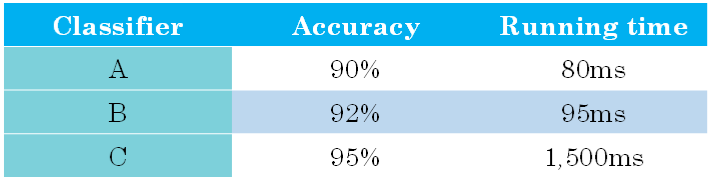
Accuracy和Running time这两个性能不太合适综合成单值评价指标。因此,我们可以将Accuracy作为优化指标(Optimizing metic),将Running time作为满意指标(Satisficing metic)。也就是说,给Running time设定一个阈值,在其满足阈值的情况下,选择Accuracy最大的模型。如果设定Running time必须在100ms以内,那么很明显,模型C不满足阈值条件,首先剔除;模型B相比较模型A而言,Accuracy更高,性能更好。
概括来说,性能指标(Optimizing metic)是需要优化的,越优越好;而满意指标(Satisficing metic)只要满足设定的阈值就好了。
五、训练集、验证集、测试集的划分 Train/dev/test distributions
一般地,我们将所有的样本数据分成三个部分:Train/Dev/Test sets。Train sets 用来训练你的算法模型;Dev sets 用来验证不同算法的表现情况,从中选择最好的算法模型;Test sets 用来测试最好算法的实际表现,作为该算法的无偏估计。
之前人们通常设置 Train sets 和 Test sets 的数量比例为70%和30%。如果有 Dev sets,则设置比例为60%、20%、20%,分别对应Train/Dev/Test sets。
这种比例分配在样本数量不是很大的情况下,例如100,1000,10000,是比较科学的。但是如果数据量很大的时候,例如100万,这种比例分配就不太合适了。科学的做法是要将 Dev sets和Test sets的比例设置得很低。因为Dev sets的目标是用来比较验证不同算法的优劣,从而选择更好的算法模型就行了。因此,通常不需要所有样本的20%这么多的数据来进行验证。对于100万的样本,往往只需要10000个样本来做验证就够了。Test sets也是一样,目标是测试已选算法的实际表现,无偏估计。对于100万的样本,往往也只需要10000个样本就够了。
因此,对于大数据样本,Train/Dev/Test sets的比例通常可以设置为98%/1%/1%,或者99%/0.5%/0.5%。样本数据量越大,相应的Dev/Test sets的比例可以设置的越低一些。
现代深度学习还有个重要的问题就是训练样本和测试样本分布上不匹配,意思是训练样本和测试样本来自于不同的分布。举个例子,假设你开发一个手机app,可以让用户上传图片,然后app识别出猫的图片。在app识别算法中,你的训练样本可能来自网络下载,而你的验证和测试样本可能来自不同用户的上传。从网络下载的图片一般像素较高而且比较正规,而用户上传的图片往往像素不稳定,且图片质量不一。因此,训练样本和验证/测试样本可能来自不同的分布。解决这一问题的比较科学的办法是尽量保证Dev sets和Test sets来自于同一分布。值得一提的是,训练样本非常重要,通常我们可以将现有的训练样本做一些处理,例如图片的翻转、假如随机噪声等,来扩大训练样本的数量,从而让该模型更加强大。即使Train sets和Dev/Test sets不来自同一分布,使用这些技巧也能提高模型性能。
最后提一点的是如果没有Test sets也是没有问题的。Test sets的目标主要是进行无偏估计。我们可以通过Train sets训练不同的算法模型,然后分别在Dev sets上进行验证,根据结果选择最好的算法模型。这样也是可以的,不需要再进行无偏估计了。如果只有Train sets和Dev sets,通常也有人把这里的Dev sets称为Test sets,我们要注意加以区别。
七、什么时候需要改变验证集/测试集和评估指标
算法模型的评价标准有时候需要根据实际情况进行动态调整,目的是让算法模型在实际应用中有更好的效果。
举个猫类识别的例子。初始的评价标准是错误率,算法A错误率为3%,算法B错误率为5%。显然,A更好一些。但是,实际使用时发现算法A会通过一些色情图片,但是B没有出现这种情况。从用户的角度来说,他们可能更倾向选择B模型,虽然B的错误率高一些。这时候,我们就需要改变之前单纯只是使用错误率作为评价标准,而考虑新的情况进行改变。例如增加色情图片的权重,增加其代价。
原来的cost function:
$J=\frac1m\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})$
更改评价标准后的cost function:
$J=\frac{1}{m}\sum_{i=1}^mw^{(i)}L(\hat y^{(i)},y^{(i)})$
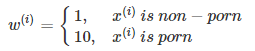
另外一个需要动态改变评价标准的情况是dev/test sets与实际使用的样本分布不一致。比如猫类识别样本图像分辨率差异:

八、可避免偏差 Avoidable bias
机器学习模型的表现通常会跟人类水平表现作比较,如下图所示:
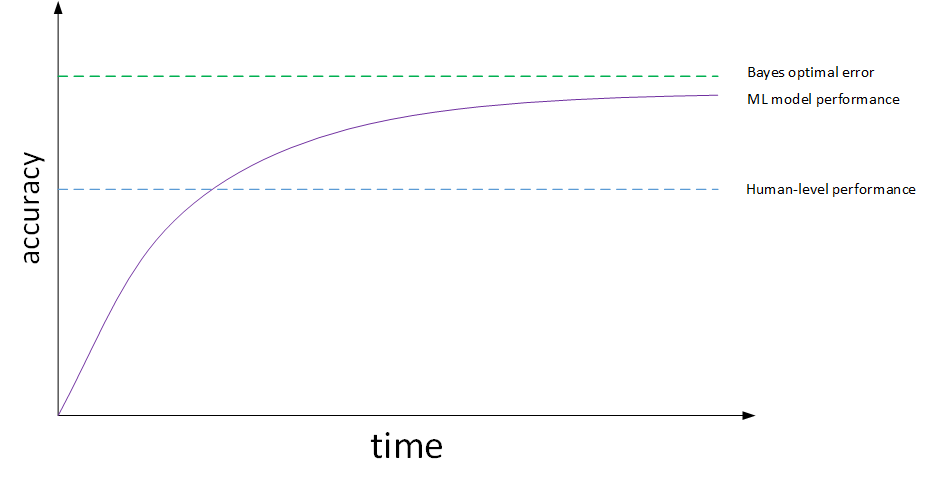
图中,横坐标是训练时间,纵坐标是准确性。机器学习模型经过训练会不断接近 human-level performance 甚至超过它。但是,超过 human-level performance 之后,准确性会上升得比较缓慢,最终不断接近理想的最优情况,我们称之为 贝叶斯最优误差 bayes optimal error。理论上任何模型都不能超过它,bayes optimal error 代表了最佳表现。
training error 与 human-level error 之间的差值称即 偏差 bias,也称作 avoidable bias ;把 dev error 与 training error 之间的差值称为 方差 variance。根据 bias 和 variance 值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
