🚁 卷积神经网络基础 Convolutional Neural Networks
一、前言
机器视觉(Computer Vision)是深度学习应用的主要方向之一。一般的 CV 问题包括以下三类:
Image Classification 图片分类
Object detection 物体识别
Neural Style Transfer 神经风格转换
下图展示了一个神经风格转换(Neural Style Transfer)的例子:

使用传统神经网络处理机器视觉的一个主要问题是输入层维度很大。例如一张 64x64x3 的图片,神经网络输入层的维度为 12288。如果图片尺寸较大,例如一张 1000x1000x3 的图片,神经网络输入层的维度将达到 3 百万,使得网络权重 W 非常庞大。这样会造成两个后果:
一是神经网络结构复杂,数据量相对不够,容易出现过拟合;
二是所需内存、计算量较大。
解决这一问题的方法就是使用卷积神经网络(CNN)。
二、卷积的含义 Convolution
卷积运算是卷积神经网络最基本的组成部分,下面我们将用 CV 中的边缘检测 Edge detection 的例子来向你说明卷积的含义。
对于CV问题,我们在之前的笔记中介绍过,神经网络由浅层到深层,分别可以检测出图片的边缘特征 、局部特征(例如眼睛、鼻子等)、整体面部轮廓:

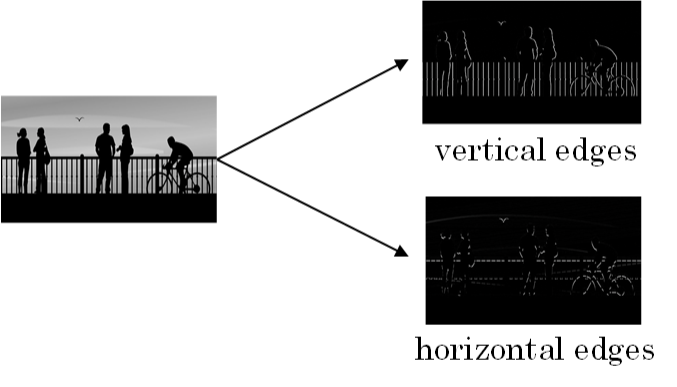
对于边缘检测,最常检测的图片边缘有两类:一是垂直边缘(vertical edges),二是水平边缘(horizontal edges)。
图片的边缘检测可以通过与相应滤波器进行卷积来实现。以垂直边缘检测为例,原始图片尺寸为6×6,滤波器filter尺寸为3×3,卷积后的图片尺寸为4×4,得到结果如下:
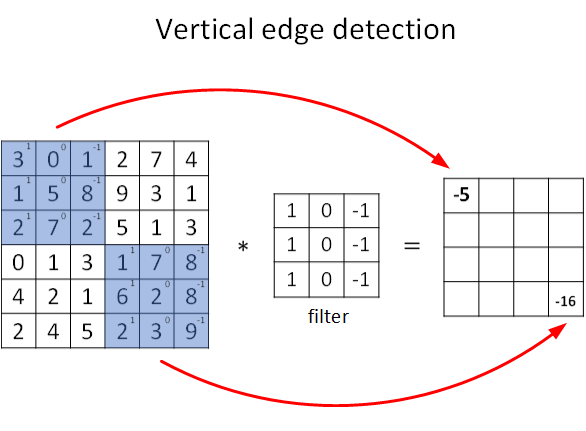
上图只显示了卷积后的第一个值和最后一个值。* 表示卷积操作。python 中,卷积用 conv_forward() 表示;tensorflow 中,卷积用 tf.nn.conv2d() 表示;keras 中,卷积用 Conv2D() 表示。
💧 下面来说明是如何计算得到这个 4×4 矩阵的。为了计算第一个元素即在4×4左上角的那个元素,使用3×3的过滤器,将其覆盖在输入图像,如下图所示。然后进行元素乘法(element-wise products)运算:
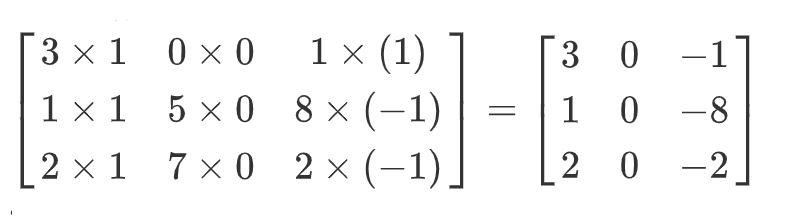
然后将该矩阵每个元素相加得到最左上角的元素,即 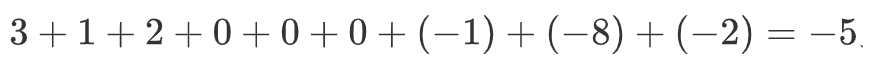
接下来,将 6x6 矩阵中的蓝色的 3x3 方块,向右移动一步,然后按照上述做法得出 4x4 矩阵的第一行的第二个元素:
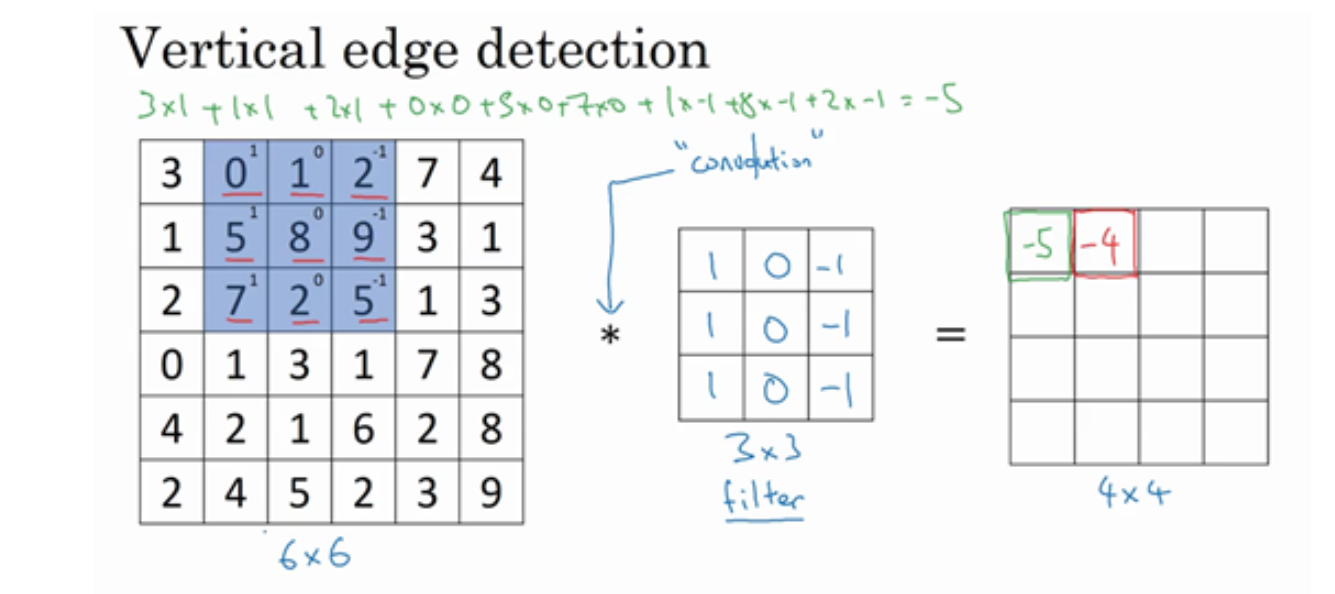
依次类推:
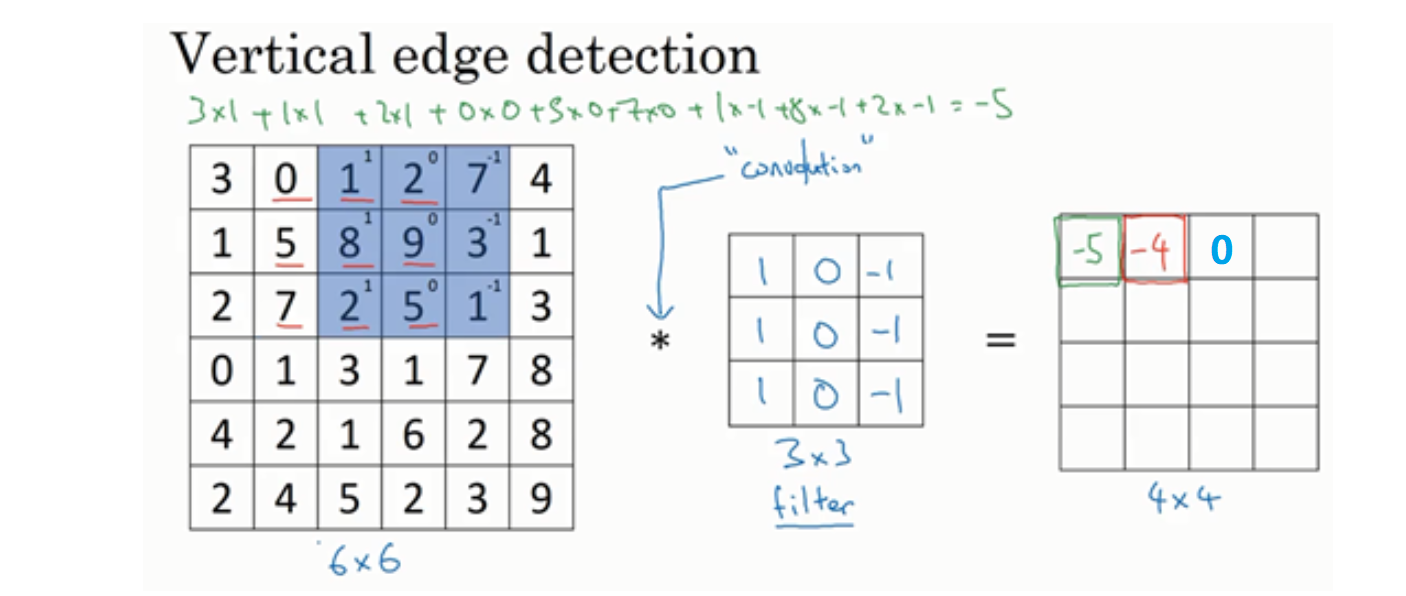

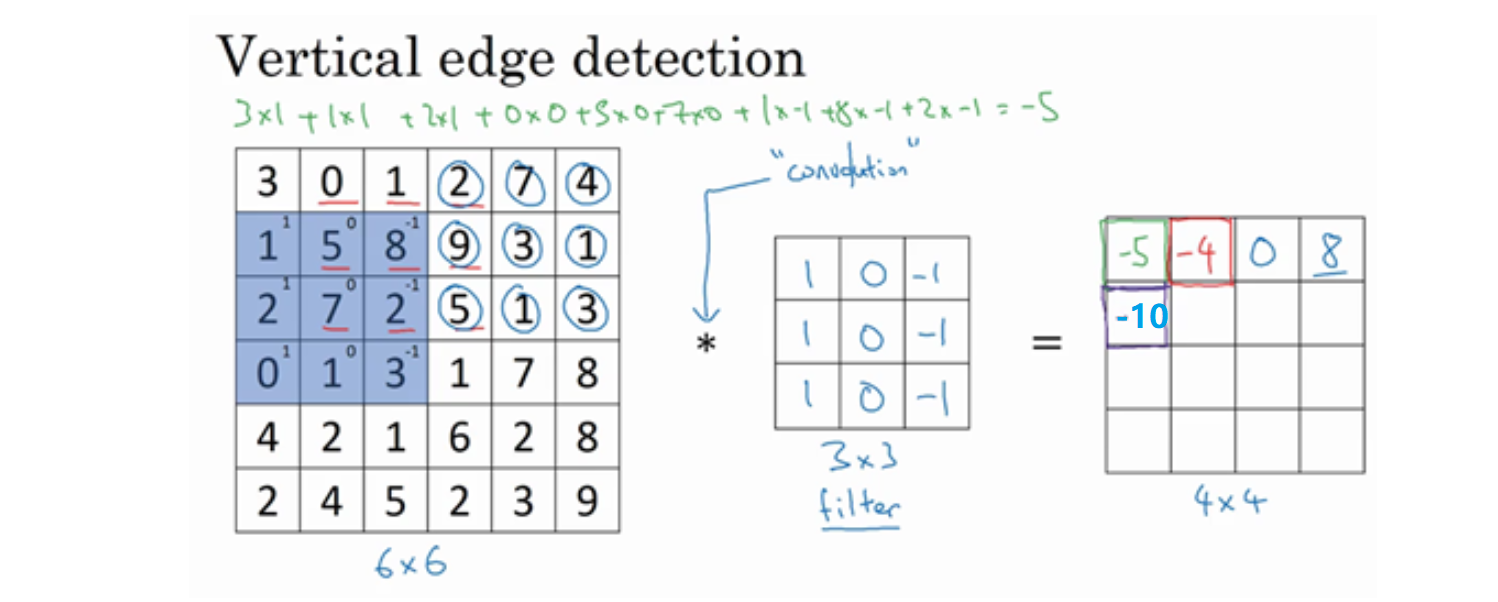
为什么这个可以做垂直边缘检测呢?让我们来看另外一个例子:

这是一个简单的6×6图像,左边的一半是10,右边一半是0。如果你把它当成一个图片,左边那部分看起来是白色的,像素值10是比较亮的像素值,右边像素值比较暗比如灰色。图片里,有一个特别明显的垂直边缘在图像中间,这条垂直线是从白色到深色的过渡线。经过卷积计算之后,这条垂直边缘就会变得很明显。
💡 当然,卷积计算也可以做水平边缘检测,垂直边缘检测和水平边缘检测的滤波器算子如下所示:
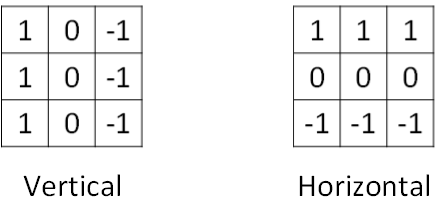
下图展示一个水平边缘检测的例子:
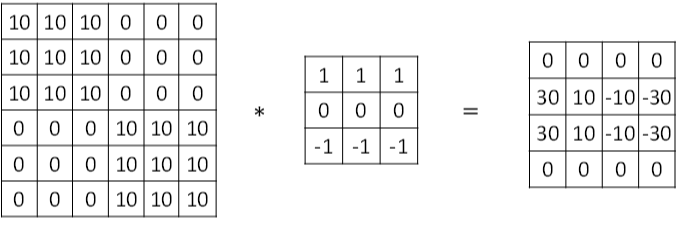
三、Padding 操作
按照我们上面讲的图片卷积,如果原始图片尺寸为n x n,filter 尺寸为f x f,则卷积后的图片尺寸为 (n-f+1) x (n-f+1),注意f一般为奇数。这样会带来两个问题:
卷积运算后,输出图片尺寸缩小
原始图片边缘信息对输出贡献得少,输出图片丢失边缘信息
为了解决图片缩小的问题,可以使用 padding 方法,即把原始图片尺寸进行扩展,扩展区域补零
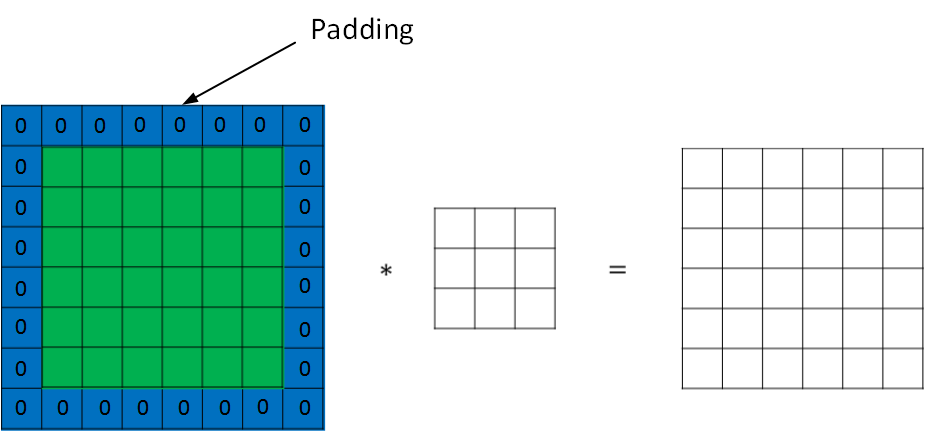
用 p 表示每个方向扩展的宽度。经过 padding 之后,原始图片尺寸为 (n+2p) x (n+2p),filter 尺寸为 f x f,则卷积后的图片尺寸为 (n+2p-f+1) x (n+2p-f+1)。若要保证卷积前后图片尺寸不变,则 p 应满足: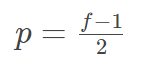
如果没有 padding 操作,即 p=0,我们称之为“Valid 卷积”;有 padding 操作,$p=\frac{f-1}{2}$ ,我们称之为“Same 卷积”。
五、卷积步长 Strided convolutions
Stride 步长 表示 filter 在原图片中水平方向和垂直方向每次的步进长度。之前我们默认 stride=1。若 stride=2,则表示 filter 每次步进长度为 2,即隔一点移动一次:
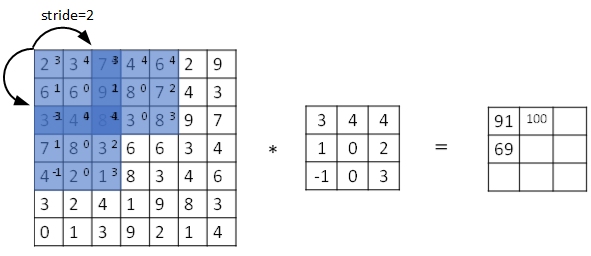
我们用s表示stride长度,p表示padding长度,如果原始图片尺寸为 n x n,filter 尺寸为 f x f,则卷积后的图片尺寸为:
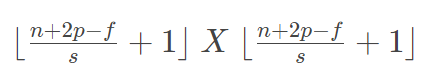
卷积运算服从结合律:
$(A * B) * C=A * (B * C)$
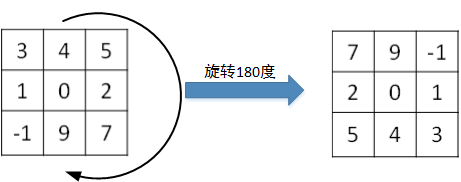
💡 事实上,严格数学意义上的卷积操作会先将 filter 绕其中心旋转180度,然后再将旋转后的 filter 在原始图片上进行滑动计算。filter旋转如下所示:
我们上述定义的卷积操作其实是互相关 cross-correlations,跳过了镜像操作,可以大大提高CNN网络运算速度,而且不影响模型性能。在深度学习文献中,按照惯例,我们将这(不进行翻转操作)叫做卷积操作。
六、三维卷积 Convolutions over volumes
对于3通道的RGB图片,其对应的滤波器算子同样也是3通道的。例如一个图片是6 x 6 x 3,分别表示图片的高度(height)、宽度(weight)和通道(#channel)。
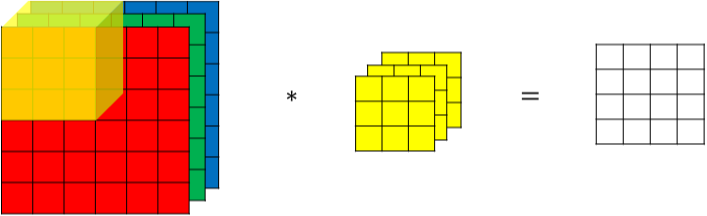
3通道图片的卷积运算与单通道图片的卷积运算基本一致。过程是将每个单通道(R,G,B)与对应的filter进行卷积运算求和,然后再将3通道的和相加,得到输出图片的一个像素值。
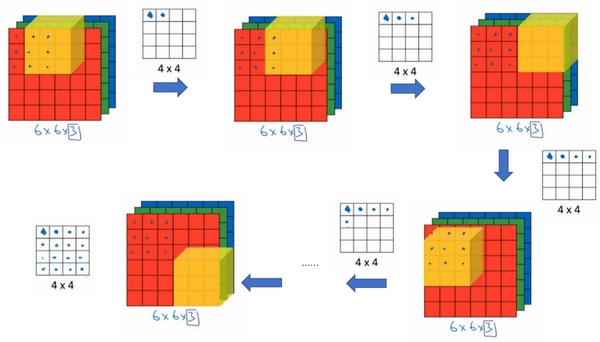
不同通道的滤波算子可以不相同。例如R通道filter实现垂直边缘检测,G和B通道不进行边缘检测,全部置零,或者将R,G,B三通道filter全部设置为水平边缘检测。
为了进行多个卷积运算,实现更多边缘检测,可以增加更多的滤波器组。例如设置第一个滤波器组实现垂直边缘检测,第二个滤波器组实现水平边缘检测。这样,不同滤波器组卷积得到不同的输出,个数由滤波器组决定。
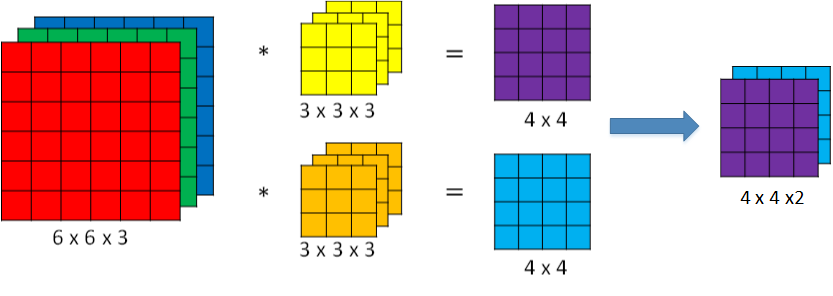
若输入图片的尺寸为 n * n * n_c,filter 尺寸为 f * f * n_c ,则卷积后的图片尺寸为 (n-f+1) * (n-f+1) * n_c’ 。其中,n_c 为图片通道数目,n_c’ 为滤波器组个数。
七、单层卷积网络 One layer of a convolutional network
卷积神经网络的单层结构如下所示:
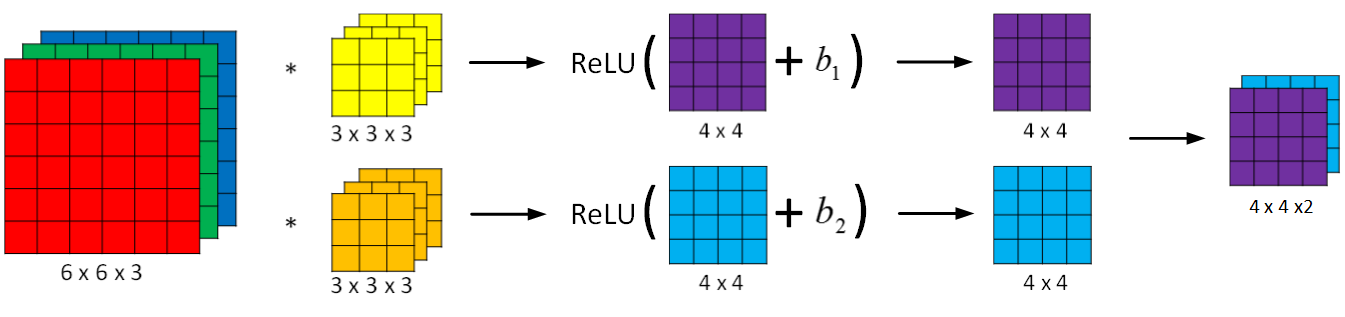
相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b。整个过程与标准的神经网络单层结构非常类似:
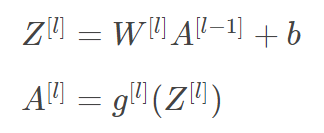
卷积运算对应着上式中的乘积运算,滤波器组数值对应着权重 $W^{[l]}$ ,所选的激活函数为 ReLU。
我们来计算一下上图中参数的数目:每个滤波器组有3x3x3=27个参数,还有1个偏移量b,则每个滤波器组有27+1=28个参数,两个滤波器组总共包含28×2=56个参数。
⭐ 我们发现,选定滤波器组后,参数数目与输入图片尺寸无关。所以,就不存在由于图片尺寸过大,造成参数过多的情况。例如一张1000x1000x3的图片,标准神经网络输入层的维度将达到3百万,而在CNN中,参数数目只由滤波器组决定,数目相对来说要少得多,这是CNN的优势之一。
📐 最后,我们总结一下 CNN 单层结构的所有标记符号,以第 l 层为例:
这一层是卷积层,用$f^{[l]}$表示过滤器大小,我们说过过滤器大小为$f×f$,上标$\lbrack l\rbrack$表示$l$层中过滤器大小为$f×f$。通常情况下,上标$\lbrack l\rbrack$用来标记$l$层。
用 $n_c^{(l)}$ 来表示第
l层过滤器的数量,等于该层图片的通道数量(所谓通道数量,举个例子:输出图像是4×4×2,说明它是二维的,则通道数量 = 过滤器数量 = 2;如果输出图像就是4×4×10,说明他是十维的,通道数量 = 过滤器数量 = 10用$p^{[l]}$来标记padding的数量,padding数量也可指定为一个valid卷积,即无padding。或是same卷积,即选定padding,如此一来,输出和输入图片的高度和宽度就相同了。
用$s^{[l]}$标记步幅。
这一层的输入会是某个维度的数据,表示为$n \times n \times n_{c}$,$n_{c}$某层上的颜色通道数。
我们要稍作修改,增加上标$\lbrack l -1\rbrack$,即$n^{\left\lbrack l - 1 \right\rbrack} \times n^{\left\lbrack l -1 \right\rbrack} \times n_{c}^{\left\lbrack l - 1\right\rbrack}$,因为它是上一层的激活值。
此例中,所用图片的高度和宽度都一样,但它们也有可能不同,所以分别用上下标$H$和$W$来标记,即$n_{H}^{\left\lbrack l - 1 \right\rbrack} \times n_{W}^{\left\lbrack l - 1 \right\rbrack} \times n_{c}^{\left\lbrack l - 1\right\rbrack}$。那么在第$l$层,图片大小为$n_{H}^{\left\lbrack l - 1 \right\rbrack} \times n_{W}^{\left\lbrack l - 1 \right\rbrack} \times n_{c}^{\left\lbrack l - 1\right\rbrack}$,$l$ 层的输入就是上一层的输出,因此上标要用$\lbrack l - 1\rbrack$。
神经网络这一层中会有输出,它本身会输出图像。其大小为$n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l]}$,这就是输出图像的大小。
前面我们提到过,这个公式给出了输出图片的大小:$\lfloor\frac{n+2p - f}{s} + 1\rfloor$(注意:($\frac{n + 2p - f}{s} +1)$直接用这个运算结果,也可以向下取整)。
在这个表达式中,$l$层输出图像的高度,即$n_{H}^{[l]} = \lfloor\frac{n_{H}^{\left\lbrack l - 1 \right\rbrack} +2p^{[l]} - f^{[l]}}{s^{[l]}} +1\rfloor$
同样我们可以计算出图像的宽度,用$W$替换参数$H$,即$n_{W}^{[l]} = \lfloor\frac{n_{W}^{\left\lbrack l - 1 \right\rbrack} +2p^{[l]} - f^{[l]}}{s^{[l]}} +1\rfloor$,公式一样,只要变化高度和宽度的参数我们便能计算输出图像的高度或宽度。

八、简单卷积网络示例
下面介绍一个简单的CNN网络模型,假设你有一张图片,你想做图片分类或图片识别,把这张图片输入定义为$x$,然后辨别图片中有没有猫,用0或1表示,这是一个分类问题,我们来构建适用于这项任务的卷积神经网络。针对这个示例,我用了一张比较小的图片,大小是39×39×3。所以$n_{H}^{[0]} = n_{W}^{[0]}$,即高度和宽度都等于39,$n_{c}^{[0]} =3$,即0层的通道数为 3(即需要 3 个过滤器):
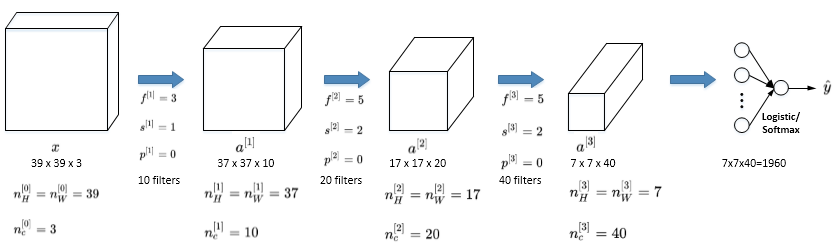
假设第一层我们用一个3×3的过滤器来提取特征,那么$f^{[1]} = 3$。$s^{[1]} = 1$,$p^{[1]} =0$,所以高度和宽度使用valid卷积。如果有10个过滤器,神经网络下一层的激活值为37×37×10,写10是因为我们用了10个过滤器,37是公式$\frac{n + 2p - f}{s} + 1$的计算结果,也就是$\frac{39 + 0 - 3}{1} + 1 = 37$,所以输出是37×37,它是一个vaild卷积,这是输出结果的大小。第一层标记为$n_{H}^{[1]} = n_{W}^{[1]} = 37$,$n_{c}^{[1]} = 10$,$n_{c}^{[1]}$等于第一层中过滤器的个数,这(37×37×10)是第一层激活值的维度。
假设还有另外一个卷积层,这次我们采用的过滤器是5×5的矩阵。在标记法中,神经网络下一层的$f=5$,即$f^{\left\lbrack 2 \right\rbrack} = 5$,步幅为2,即$s^{\left\lbrack 2 \right\rbrack} = 2$。padding为0,即$p^{\left\lbrack 2 \right\rbrack} = 0$,且有20个过滤器。所以其输出结果会是一张新图像,这次的输出结果为17×17×20,因为步幅是2,维度缩小得很快,大小从37×37减小到17×17,减小了一半还多,过滤器是20个,所以通道数也是20,17×17×20即激活值$a^{\left\lbrack 2 \right\rbrack}$的维度。因此$n_{H}^{\left\lbrack 2 \right\rbrack} = n_{W}^{\left\lbrack 2 \right\rbrack} = 17$,$n_{c}^{\left\lbrack 2 \right\rbrack} = 20$。
我们来构建最后一个卷积层,假设过滤器还是5×5,步幅为2,即$f^{\left\lbrack 2 \right\rbrack} = 5$,$s^{\left\lbrack 3 \right\rbrack} = 2$,最后输出为7×7×40,假设使用了40个过滤器。padding为0,40个过滤器,最后结果为7×7×40。
到此,这张39×39×3的输入图像就处理完毕了,为图片提取了7×7×40个特征,计算出来就是1960个特征。然后对该卷积进行处理,将 $a^{[3]}$ 排列成1列,维度为1960 x 1,对应着参数 $W$,然后连接最后一级输出层。输出层可以是一个神经元,即二元分类(logistic);也可以是多个神经元,即多元分类(softmax)。最后得到预测输出 $\hat y$ 。
值得一提的是,随着CNN层数增加,$n_H^{[l]}$ 和 $n_W^{[l]}$ 一般逐渐减小,而 $n_c^{[l]}$ 一般逐渐增大。
🚩 CNN有三种类型的 layer:
卷积层 / Convolution 层(CONV)
池化层 / Pooling 层(POOL)
全连接层 / Fully connected 层(FC)
CONV 最为常见也最重要,关于POOL和FC我们之后再介绍。
九、池化层 Pooling layers
Pooling layers 是CNN中用来减小尺寸,提高运算速度的,同样能减小noise影响,让各特征更具有健壮性。
① Max Pooling
Pooling layers的做法比 convolution layers 简单许多,没有卷积运算,仅仅是在滤波器算子滑动区域内取最大值,即 max pooling,这是最常用的做法。注意,超参数 p 很少在pooling layers中使用。
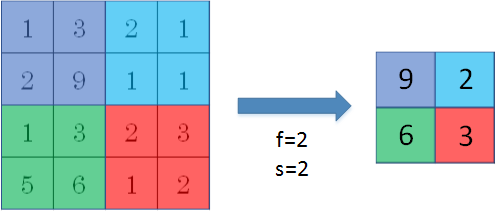
Max pooling 的好处是只保留区域内的最大值(特征),忽略其它值,降低noise影响,提高模型健壮性。而且,max pooling需要的超参数仅为滤波器尺寸 f 和滤波器步进长度s,没有其他参数需要模型训练得到,计算量很小。
如果是多个通道,那么就每个通道单独进行 max pooling 操作。
② Average Pooling
除了 max pooling 之外,还有一种做法:average pooling。顾名思义,average pooling 就是在滤波器算子滑动区域计算平均值。
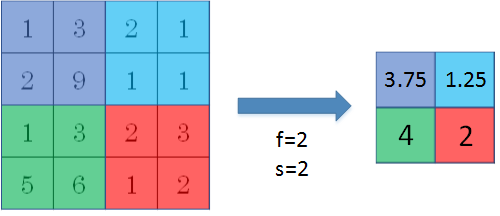
实际应用中,max pooling 比 average pooling 更为常用。
十、卷积神经网络示例 Convolutional neural network
构建全卷积神经网络的构造模块我们已经掌握得差不多了,下面来看个例子:

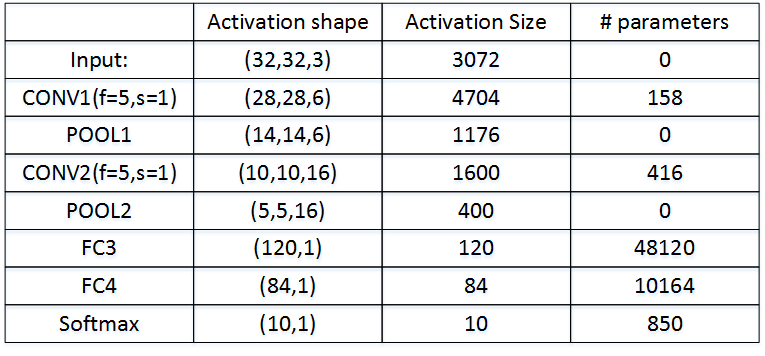
图中,CON层后面紧接一个POOL层,CONV1和POOL1构成第一层 Layer 1,CONV2和POOL2构成第二层。特别注意的是FC3和FC4为全连接层FC,它跟标准的神经网络结构一致。最后的输出层(softmax)由10个神经元构成。
整个网络各层的尺寸和参数如下表格所示:
十一、为什么使用卷积神经网络
相比标准神经网络,CNN的优势之一就是参数数目要少得多。参数数目少的原因有两个:
参数共享:一个特征检测器(例如垂直边缘检测)对图片某块区域有用,同时也可能作用在图片其它区域。
连接的稀疏性:因为滤波器算子尺寸限制,每一层的每个输出只与输入部分区域内有关。
除此之外,由于CNN参数数目较小,所需的训练样本就相对较少,从而一定程度上不容易发生过拟合现象。而且,CNN 比较擅长捕捉区域位置偏移。也就是说CNN进行物体检测时,不太受物体所处图片位置的影响,增加检测的准确性和系统的健壮性。